Hemmes mathematische Rätsel: Wie lang ist die Seite?
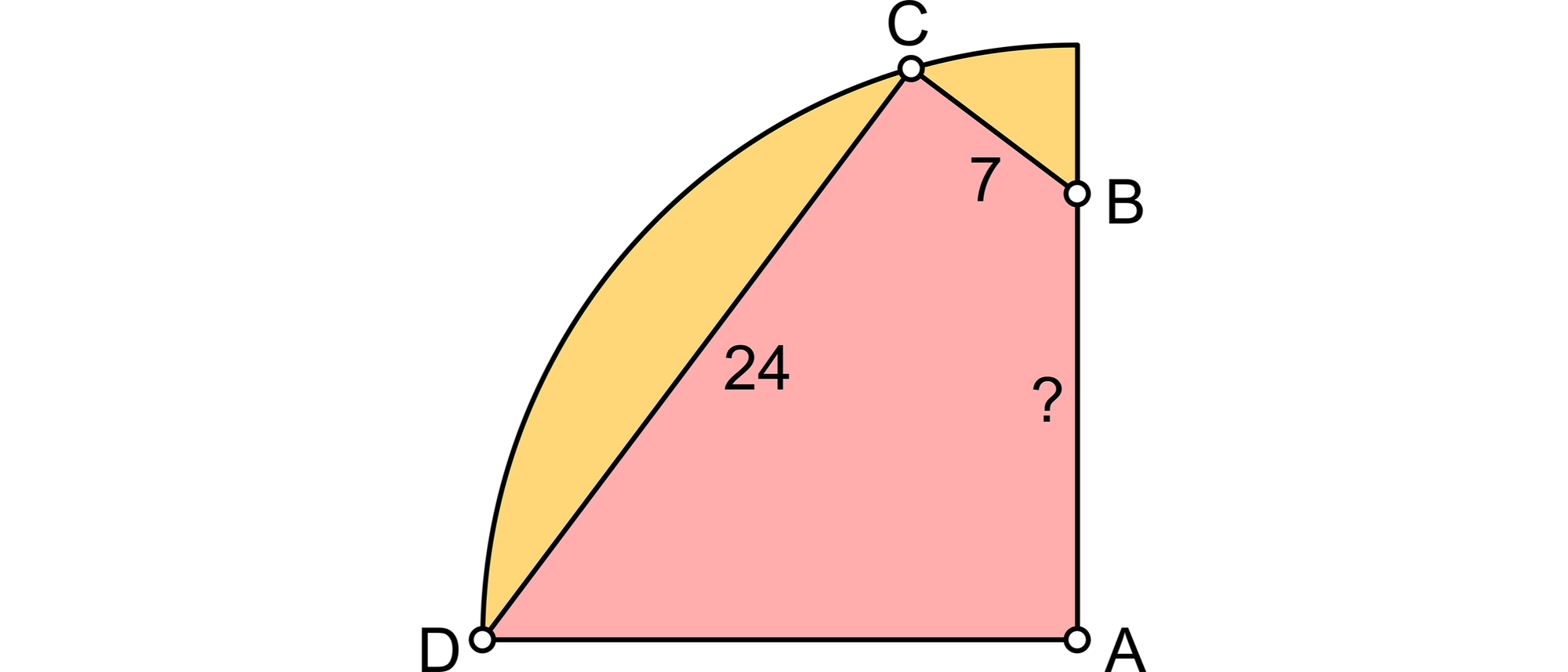
Das Viereck ABCD liegt, so wie es in dem Bild zu sehen ist, in einem Viertelkreis. An den beiden Ecken A und C hat es rechte Winkel. Eine seiner Seiten ist ein Viertelkreisradius, eine hat die Länge 7 und eine die Länge 24. Wie lang ist die mit einem Fragezeichen markierte Seite?
Ergänzt man den Viertelkreis zu einem Halbkreis und verlängert die Strecke BC nach rechts unten, so trifft sie nach dem Satz des Thales im Punkt E auf den Halbkreisdurchmesser und den Halbkreisumfang. Das Dreieck BDE ist gleichschenklig. Seine Schenkel haben nach dem Satz des Pythagoras die Länge BD = BE = √(BC2 + CD2) = √(72 + 242) = √625 = 25. Folglich hat die Strecke CE die Länge CE = BC + BE = 7 + 25 = 32. Das Dreieck CDE ist rechtwinklig und hat eine Hypotenuse der Länge DE = 2r = √(242 + 322) = √1600 = 40. Daraus erhält man schließlich die gesuchte Länge der Kathete AB des rechtwinkligen Dreiecks ABD zu AB = √(252 – 202) = √225 = 15.
Schreiben Sie uns!
2 Beiträge anzeigen