Hemmes mathematische Rätsel: Wie viel Prozent machen die Viertelkreise aus?
© Heinrich Hemme (Ausschnitt)
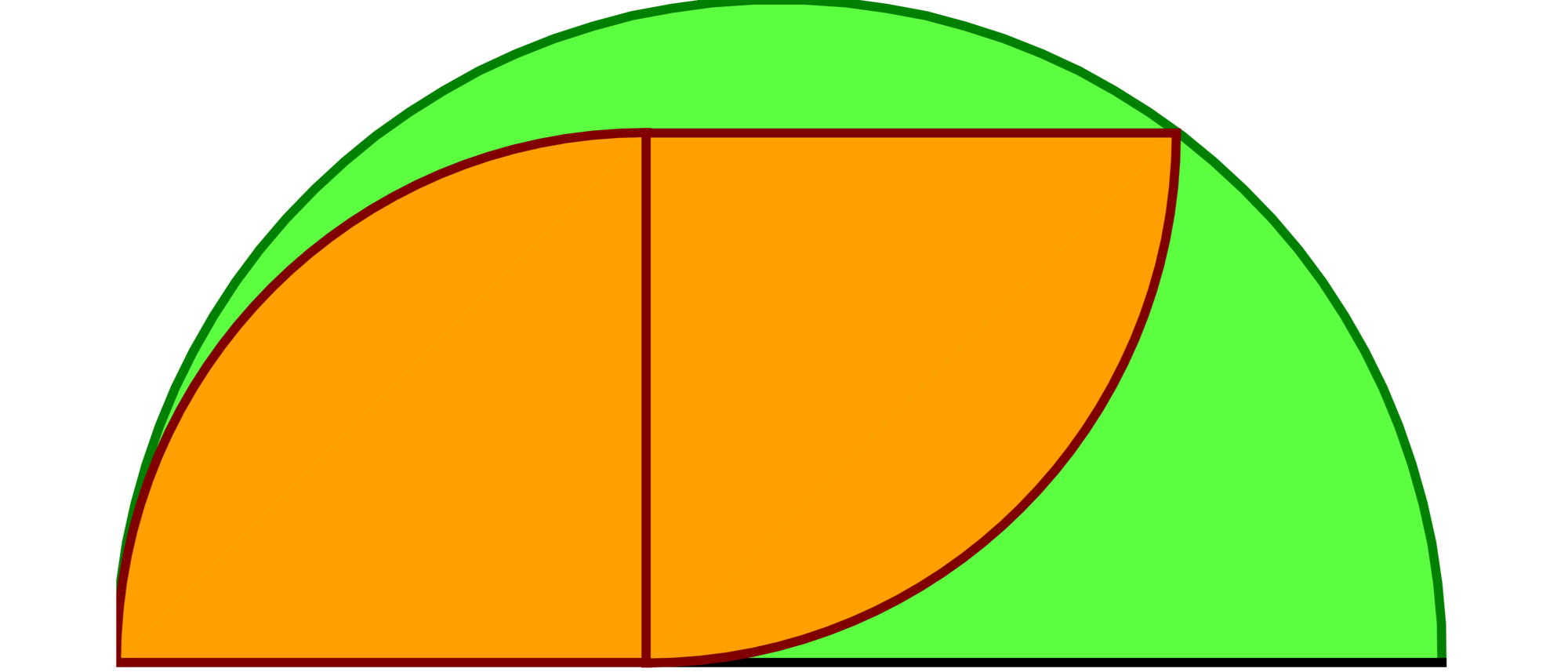
In einem Halbkreis stecken zwei Viertelkreise. Wie viel Prozent der Halbkreisfläche decken sie ab?
Nach dem Satz des Thales ist das Dreieck ABC rechtwinklig. Folglich sind die beiden Dreiecke ABD und BCD ähnlich. Damit gilt für die Kathetenverhältnisse CD/BD = BD/AD. Hat der Halbkreis den Radius R und jeder der beiden Viertelkreise den Radius r, kann man für das Kathetenverhältnis auch 2r/r = r/(2R – 2r) schreiben, was sich zu r/R = 4/5 vereinfachen lässt. Das Verhältnis der beiden Viertelkreisflächen zur Halbkreisfläche beträgt (2 · 1/4πr2)/(1/2πR2) = (r/R)2 = (4/5)2 = 16/25 = 0,64. Die Viertelkreise decken folglich 64 Prozent des Halbkreises ab.
© Heinrich Hemme (Ausschnitt)
Schreiben Sie uns!
2 Beiträge anzeigen