Hemmes mathematische Rätsel: Wie viele Möglichkeiten gibt es?
Henry Ernest Dudeney war wohl der bedeutendste Rätselerfinder, der jemals lebte. Er wurde 1857 in Mayfield in England als Sohn eines Dorfschullehrers geboren und starb 1930. Dudeney entwarf über Jahrzehnte für zahlreiche Zeitungen und Magazine regelmäßig Denksportprobleme. Er fasste die meisten seiner Rätsel später auch zu Büchern zusammen. Die heutige Kopfnuss stammt aus seinem 1917 erschienenen Buch »Amusements in Mathematics«.
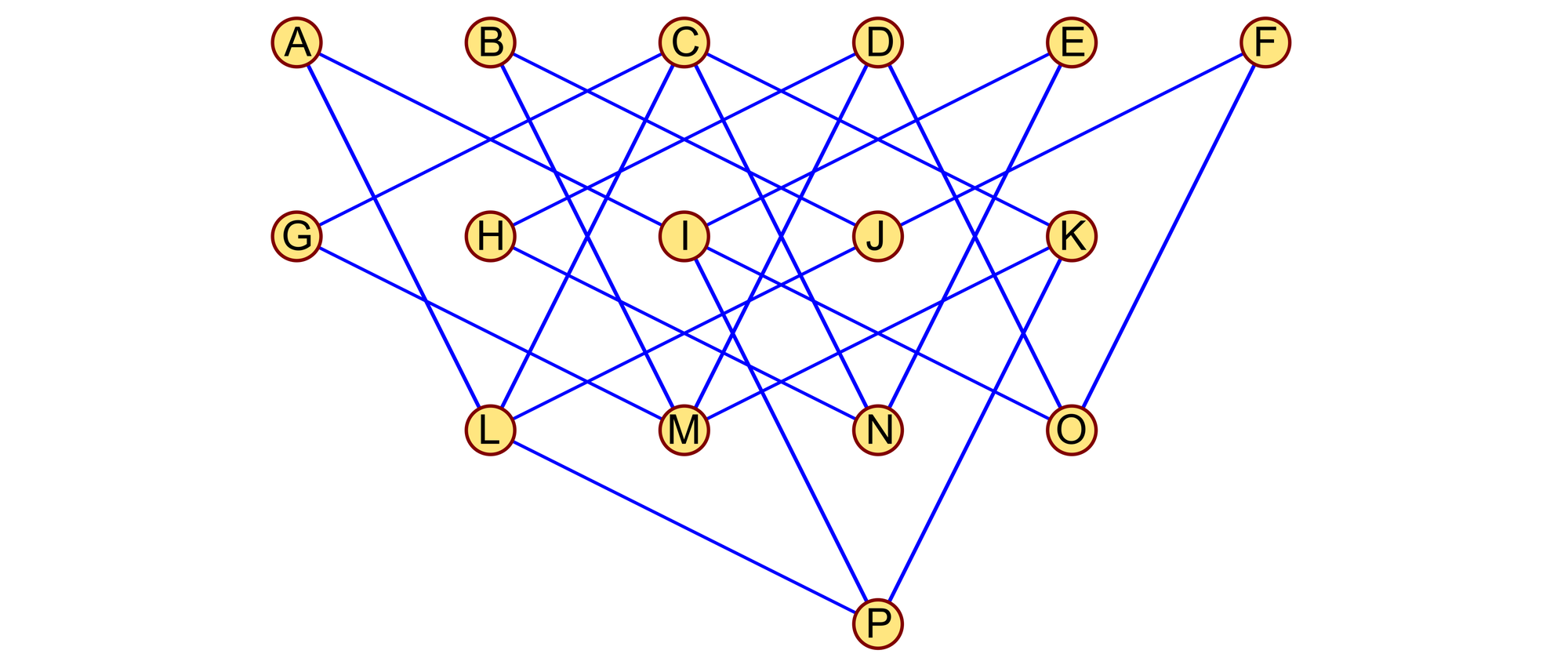
Ein Handlungsreisender, der in der Stadt A wohnt, will im Laufe einer Woche alle Städte von B bis P besuchen, wenn auch nicht unbedingt in dieser Reihenfolge, und zum Schluss wieder nach A zurückkehren. Dabei möchte er jede Stadt nur genau einmal betreten. Die blauen Linien sind die einzigen Straßen zwischen den 16 Städten. Der Handlungsreisende darf nur die geraden Verbindungen zwischen zwei Städten benutzen und nicht an den Kreuzungen zweier Straßen abbiegen. Wie viele verschiedene Rundreisen sind so möglich?
Fährt der Handlungsreisende über eine Straße in eine Stadt hinein, muss er sie über eine andere wieder verlassen. Damit eine Rundreise überhaupt möglich ist, müssen also in jede Stadt mindestens zwei Straßen führen. In die Städte A, B, E, F, G und H führen genau zwei Straßen. Über diese Straßen muss der Handlungsreisende also auf jeden Fall fahren. Dadurch liegt aber auch schon fest, über welche Straßen er die Städte I, J, M und N erreicht und verlässt. Anschließend sind auch noch die restlichen Verbindungen eindeutig. Es gibt somit nur eine mögliche Rundtour A-I-E-N-H-D-O-F-J-B-M-G-C-K-P-L-A für den Handlungsreisenden, die er aber in zwei verschiedenen Richtungen durchfahren kann.
Schreiben Sie uns!
Beitrag schreiben