Hemmes mathematische Rätsel: Wohin müssen die Zahlen?

Verteilen Sie die Zahlen 1/6, 1/3, 1/2, 2/3, 1, 3/2, 2, 3 und 6 so auf die neun Felder des Quadrates, dass das Produkt der drei Zahlen jeder Zeile, jeder Spalte und der beiden Diagonalen gleich groß ist.

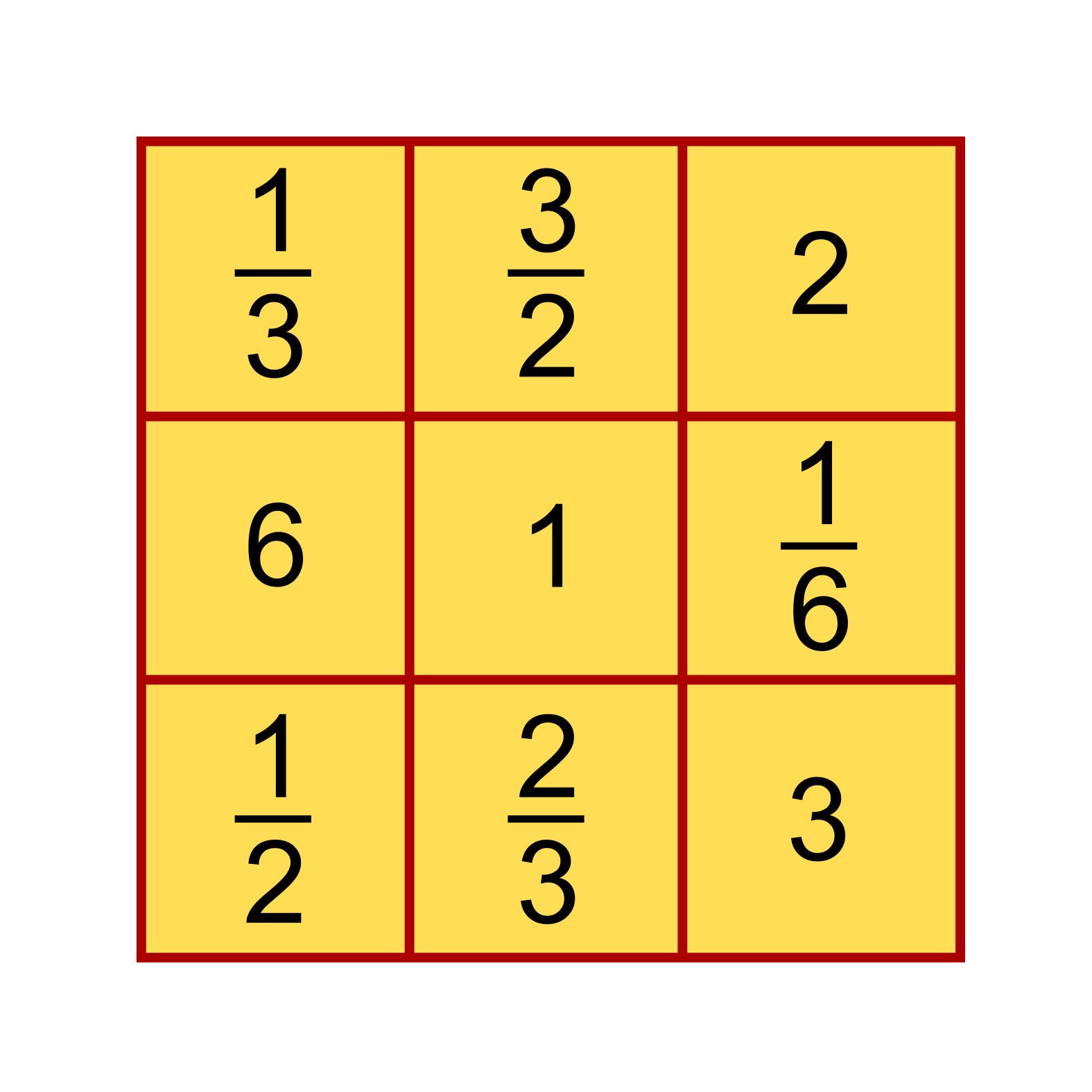
Da das Produkt aller neun Zahlen 1/6 · 1/3 · 1/2 · 2/3 · 1 · 3/2 · 2 · 3 · 6 = 1 ist, muss auch das Produkt in jeder der acht Reihen 1 sein. Es gibt insgesamt acht Möglichkeiten dafür, dass drei dieser Zahlen das Produkt 1 ergeben. Diese sind 1/6 · 1 · 6, 1/6 · 2 · 3, 1/3 · 1/2 · 6, 1/3 · 1 · 3, 1/3 · 3/2 · 2, 1/2 · 2/3 · 3, 1/2 · 1 · 2 und 2/3 · 1 · 3/2. Das Mittelfeld des Quadrates gehört zu vier Reihen. Da 1 die einzige Zahl ist, die in vier Möglichkeiten vorkommt, muss sie auf dem Mittelfeld stehen. Die Eckfelder des Quadrates gehören zu jeweils drei Reihen, und weil nur 1/3, 1/2, 2 und 3 je dreimal vorkommen, müssen diese Zahlen auf den Eckfeldern stehen. Der Rest ist einfach. Abgesehen von Spiegelungen und Drehungen des Musters ist die Lösung eindeutig.







Schreiben Sie uns!
Beitrag schreiben