Von Nicole Oresme weiß man, dass er um 1323 in Allemagne (heute: Fleury-sur-Orne) geboren wurde, einer Ortschaft in der Nähe von Caen (Normandie). Zu Beginn der 1340er Jahre studiert er Artes am Collège de Navarre, einer königlichen Einrichtung für Studenten, die nicht in der Lage sind, Studiengelder zu bezahlen. 1348 nimmt er ein Studium der Theologie an der Universität Paris auf. 1356 wird er zum Leiter (grand-maître) des Collège de Navarre ernannt. Nach seiner Promotion (1362) folgt die Ernennung zum Domherrn an der Sainte-Chapelle in Paris, später auch zum Dekan der Kathedrale von Rouen. Oresme freundet sich mit dem Dauphin Charles an, der ihn im Jahr 1364 nach seiner Inthronisation als König Charles V zum Hofkaplan und zu seinem persönlichen Berater ernennt. 1377 wird er vom König als Bischof von Lisieux eingesetzt. Lisieux ist heute ein Ort mit nur 20 000 Einwohnern, in der Römerzeit und im Mittelalter war es ein wichtiges regionales Zentrum, zwischen Caen und Rouen gelegen. Das Bischofsamt nimmt Oresme bis zu seinem Tod im Jahr 1382 wahr.

Nicole Oresme gilt als einer der bedeutendsten Gelehrten des späten Mittelalters. Im Auftrag des Königs übersetzt er verschiedene Werke des Aristoteles ins Französische; hierfür "erfindet" er einige neue Begriffe, die seitdem zum Wortschatz der französischen Sprache gehören. Aus seinen Kommentaren zu den übersetzten Schriften wird deutlich, dass eine neue Zeit begonnen hat, in der die bisher unreflektiert übernommenen Ansichten antiker Philosophen kritisch überdacht werden.

Zu Oresmes Lehrern gehört Jean Buridan, der sich unter anderem mit der Bewegungstheorie des Aristoteles auseinandergesetzt hatte. Gemäß dieser Theorie ist eine ständige Kraft erforderlich, um die Bewegung eines Objekts aufrecht zu erhalten. Eine solche wird durch das umgebende Medium ausgeübt; im Vakuum ist daher keine Bewegung möglich. Buridan modifiziert diese Theorie durch die Einführung eines Impetus als Bewegungsursache – nachdem der Körper einen "Anstoß" erhalten hat, wird dieser vom bewegten Körper "aufgebraucht".

Oresme geht in seiner Schrift De configurationibus qualitatum et motuum über diese Ansätze Buridans hinaus und versucht, Bewegungsabläufe durch Diagramme zu veranschaulichen. Er unterscheidet dabei extensio und intensio als zugehörige Eigenschaften – konkret bei der Bewegung eines Körpers die Zeit als extensio (Ausdehnung) und die Geschwindigkeit als intensio.

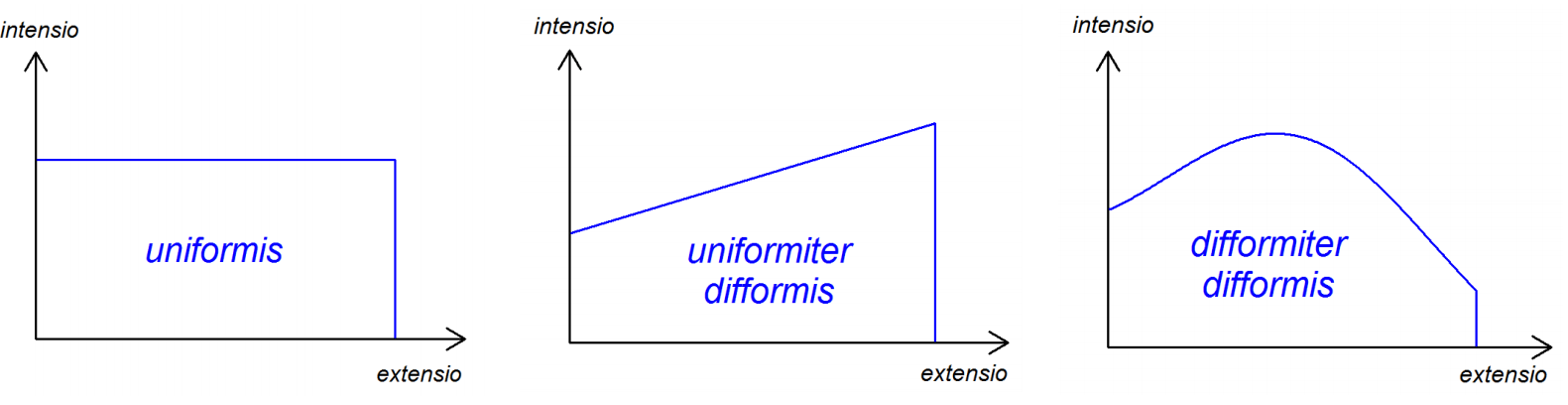
In einer Art Koordinatensystem stellt er unterschiedliche Bewegungsformen dar: Eine gleichförmige Bewegung (uniformis) mithilfe einer Geraden, die parallel zur Zeitachse verläuft, eine gleichförmig beschleunigte Bewegung, also eine Bewegung, bei der die Geschwindigkeit in gleichen Zeitabschnitten um jeweils den gleichen Betrag zunimmt (uniformiter difformis), mithilfe einer ansteigenden Gerade, sowie eine Bewegung, bei der sich die Geschwindigkeit nicht gleichförmig verändert (difformiter difformis).

Dass Oresme einen Zusammenhang zwischen dem Flächeninhalt der in der Grafik dargestellten Fläche und dem in der Bewegung zurückgelegtem Weg erkennt, wird aus seiner Schrift Tractatus de configuratione intensionum deutlich. Am Merton-College der Universität Oxford war um 1328 von den Gelehrten Thomas Bradwardine und Richard Swineshead die sogenannte Merton-Regel aufgestellt worden:

Wird ein Körper in einem gewissen Zeitintervall gleichmäßig von einer Geschwindigkeit \(v_0\) auf eine Geschwindigkeit \(v_1\) beschleunigt, dann legt der Körper in diesem Zeitintervall denselben Weg zurück wie ein Körper, der sich mit der Geschwindigkeit \(\frac{1}{2}\cdot(v_0+v_1)\) bewegt.

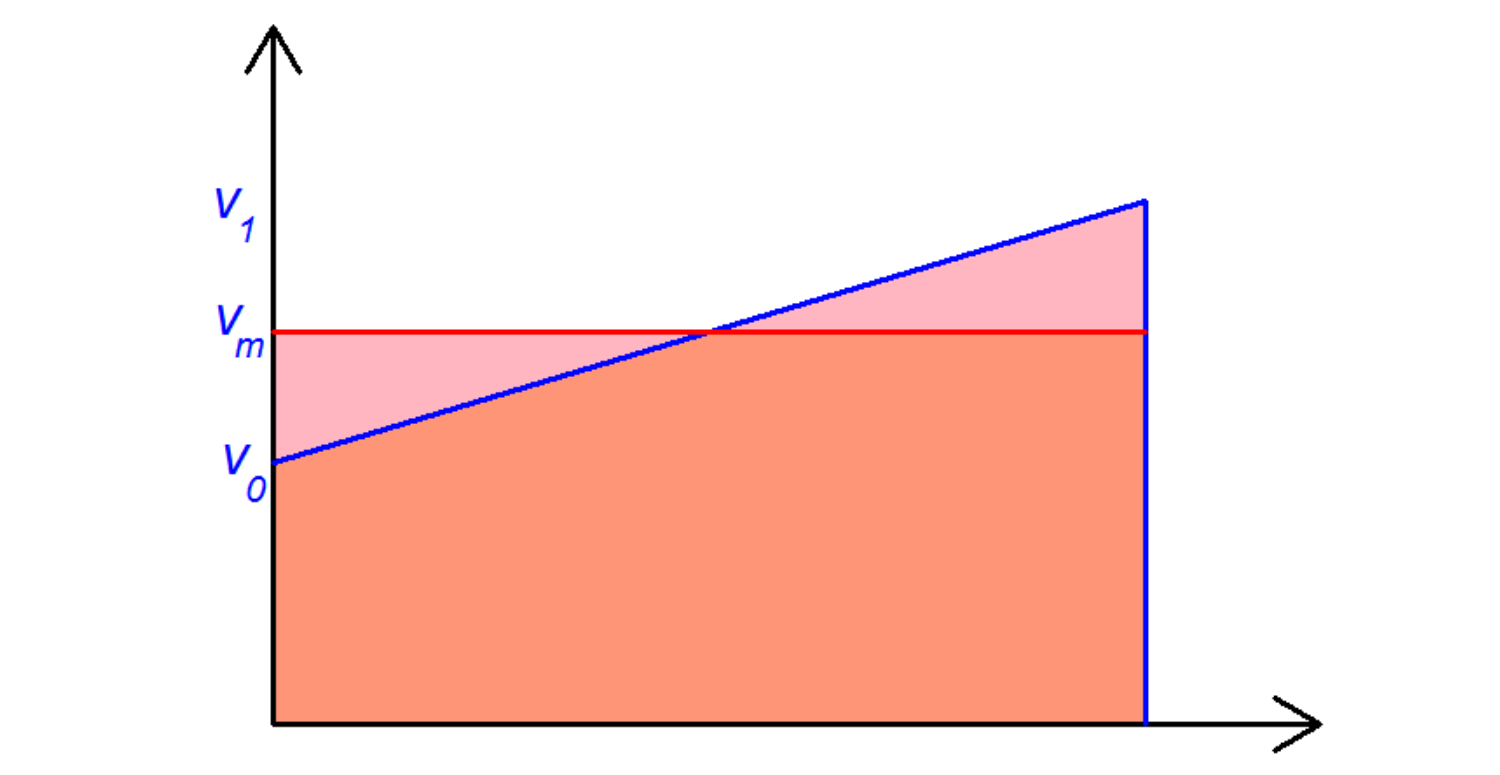
Die Gültigkeit dieser Regel – von den Oxford-Gelehrten wortreich plausibel gemacht – kann von Oresme leicht mithilfe der zweiten Grafik begründet werden. Im Tractatus de configuratione intensionum heißt es: Jede gleichförmigerweise ungleichförmige Qualität hat dieselbe Quantität, als wenn sie gleichförmig demselben Objekt zukommen würde mit dem Grade des mittleren Punktes. Der Universalgelehrte Oresme beschäftigt sich auch mit der Frage, welche musikalischen Intervalle "schön" (pulcher) und welche "hässlich" (turpis) klingen und welche Teilungsverhältnisse auf den Saiten für die Töne gewählt werden sollten. In diesem Zusammenhang entwickelt er die klassische Lehre der Proportionen weiter. Seine Schriften Algorismus proportionum und De proportionibus proportionum beispielsweise enthalten die Anleitung, wie man zu einem gegebenen Zahlenverhältnis \(b_1 : b_2\) Zahlen \(a_1\) und \(a_2\) findet, für die \(b_1 : a_1 = a_1 : a_2 = a_2 : b_2\) gilt. In der heute üblichen Schreibweise würde man dies mithilfe von gebrochenen Exponenten notieren: \( \frac{a_1}{a_2}=\left(\frac{b_1}{b_2}\right)^{\frac{1}{3}} \). Auch gibt er Rechenregeln zum Umgang mit diesem Typ von Proportionen an.

Nur zwei seiner Schriften verfasst Oresme in französischer Sprache: Traité de la sphère und Traité du ciel et du monde. Hier legt er dar, dass man weder durch Beobachtung noch durch Experimente entscheiden könne, ob sich die Erde oder der Himmel dreht, und er widerlegt die Argumente, die Aristoteles einst angeführt hatte, um zu begründen, warum sich die Erde nicht bewegen könne. Gleichwohl neigt er dazu, dass das geozentrische Weltbild wohl richtig ist.

Grundsätzlich vertritt er aber die Ansicht, dass Erscheinungen in der Natur natürliche Erklärungen haben müssen, und er wendet sich scharf gegen jede Form des Okkultismus und gegen den Versuch der Astrologen, aus der Stellung der Planeten Aussagen über zukünftige Ereignisse und Schicksale ableiten zu können.

In seinem Buch zum Geldwesen (De origine, natura, jure et mutationibus monetarum) bestreitet Oresme das Recht der Herrschenden, Münzen zu prägen. Vielmehr gehöre das Geld der Bevölkerung, die nämlich ansonsten darunter zu leiden hat, wenn die Herrscher durch unkontrollierte Münzprägungen den Wert der Münzen mindern.

Seiner Zeit voraus ist Oresme auch bei der Behandlung von unendlichen Reihen. In den Questiones super geometriam Euclidis zeigt er, dass sich die Terme geometrischer Reihen auf einfache Weise darstellen lassen, zum Beispiel \( \frac{1}{2} +\left(\frac{1}{2}\right)^2+\left(\frac{1}{2}\right)^3+...+\left(\frac{1}{2}\right)^n=1-\left(\frac{1}{2}\right)^n \).

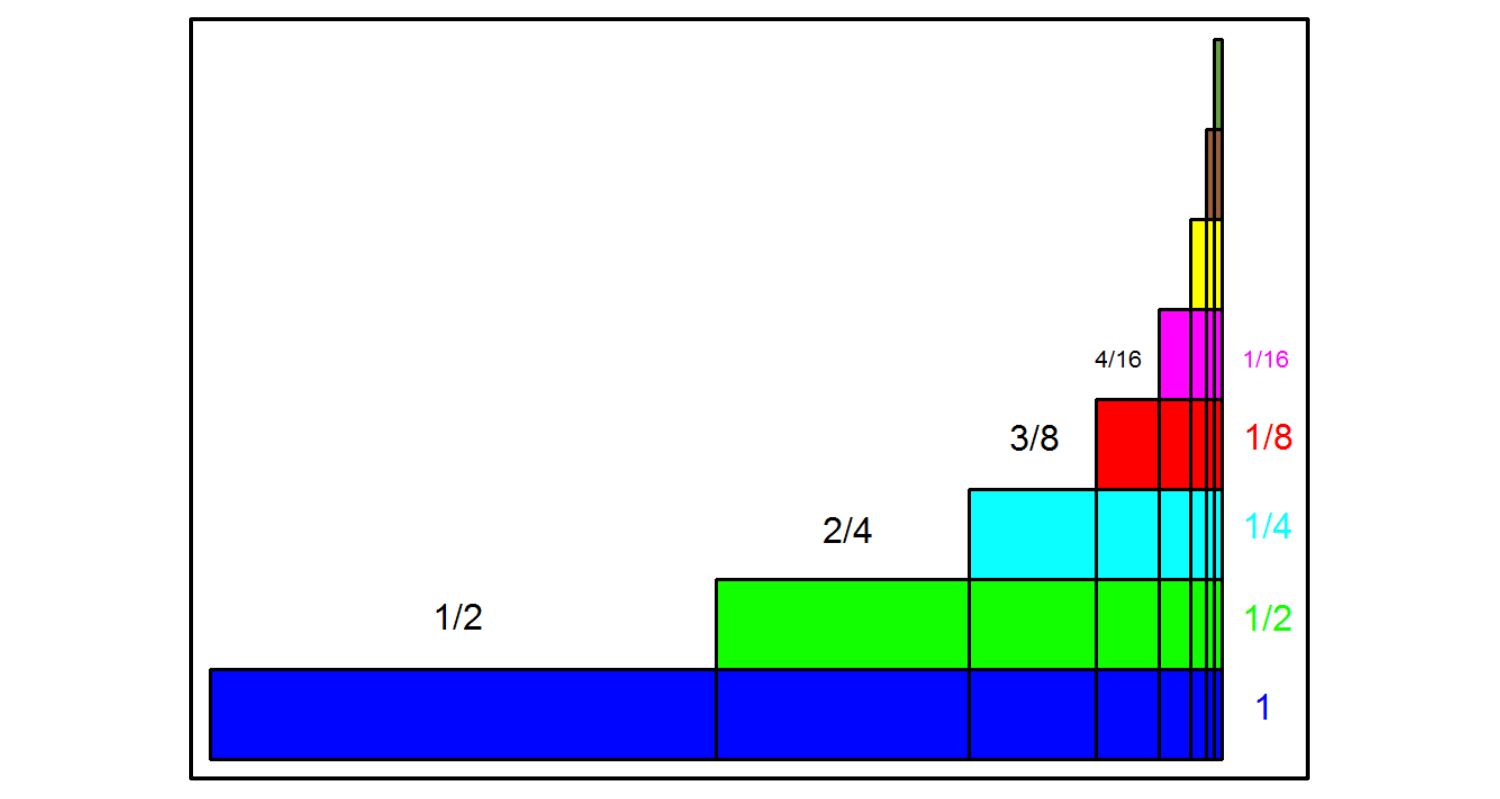
Durch eine geschickte Umordnung leitet er hieraus her, dass auch folgende Gleichung gilt: \(\frac{1}{2}+\frac{2}{4}+\frac{3}{8}+...+\frac{n}{2^n}=1+\left(1-\left(\frac{1}{2}\right)^n\right)=2-\left(\frac{1}{2}\right)^n \).

Und da sich der Term rechts mit wachsendem \(n\) dem Wert 2 nähert, gilt dies auch für: \(\frac{1}{2}+\frac{2}{4}+\frac{3}{8}+...+\frac{n}{2^n}\).

Oresme ist der Erste, der beweist, dass die Teilsummen \( H_n=1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{n-1}+\frac{1}{n} \) der so genannten harmonischen Reihe über alle Grenzen hinauswachsen, diese also im Unterschied zu den betrachteten geometrischen Reihen nicht konvergent ist. Sein genialer Einfall besteht darin, zunächst 2, dann weiter 4, 8, 16, ... Stammbrüche zusammenzufassen und diese jeweils nach unten durch den Wert 0,5 abzuschätzen, so dass auf der linken Seite des Ungleichheitszeichens Teilsummen der harmonischen Reihe \(H_n\) stehen mit \(n = 2^k\) und auf der rechten Seite die Glieder einer divergenten linearen Folge \(a_k\) mit \(a_k=1+\frac{1}{2}\cdot k\). Daher divergiert die harmonische Reihe.

\( H_4=1+\frac{1}{2}+\left(\frac{1}{3}+\frac{1}{4}\right) > 1 + \frac{1}{2 }+\left(\frac{1}{4}+\frac{1}{4}\right) = 2 =a_2\)

\( H_8=1+\frac{1}{2}+\left(\frac{1}{3}+\frac{1}{4}\right)+\left(\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}\right) \)
\(\ \ \ \ > 1+\frac{1}{2}+\left(\frac{1}{4}+\frac{1}{4}\right)+\left(\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}\right) = 2,5 =a_3\)

\( H_{16}=1+\frac{1}{2}+\left(\frac{1}{3}+\frac{1}{4}\right)+\left(\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}\right)\)
\(\ \ \ \ \ \ + \left(\frac{1}{9}+\frac{1}{10}+\frac{1}{11}+\frac{1}{12}+\frac{1}{13}+\frac{1}{14}+\frac{1}{15}+\frac{1}{16}\right)\)
\(\ \ \ \ > 1+\frac{1}{2}+\left(\frac{1}{4}+\frac{1}{4}\right)+\left(\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}\right) \)
\(\ \ \ \ \ \ \ + \left(\frac{1}{16}+\frac{1}{16}+\frac{1}{16}+\frac{1}{16}+\frac{1}{16}+\frac{1}{16}+\frac{1}{16}+\frac{1}{16}\right) = 3 =a_4\) ...