Konflikte sind in der Regel nichts Gutes. Sie können Personen von ihren eigentlichen Tätigkeiten ablenken oder gar ganz lähmen. Daher sollte man meinen, dass Streit den wissenschaftlichen Fortschritt bremst. Was hätten Leibniz und Newton nicht noch alles entdeckt, wenn sie ihre Plagiatsvorwürfe begraben und stattdessen gemeinsam geforscht hätten? Eine Antwort auf diese Frage werden wir wohl nie bekommen.

Doch tatsächlich kann Zwietracht manchmal auch die Forschung befeuern. Das zeigt sich insbesondere an den Brüdern Johann und Jakob Bernoulli. Ihre Unstimmigkeiten und ihr Drang, sich gegenseitig zu beweisen und zu übertrumpfen, führte dazu, dass sie sich immer schwierigeren Fragestellungen widmeten. Mit Erfolg: Beide brachten die Mathematik weit voran. Und tatsächlich bildet eine Idee von Johann Bernoulli inzwischen das mathematische Fundament einer jeden physikalischen Theorie – von der newtonschen Mechanik über die allgemeine Relativitätstheorie bis hin zum Standardmodell der Teilchenphysik.

Dabei war die Beziehung der Brüder anfangs friedlich. Der zwölf Jahre ältere Jakob brachte seinem kleinen Bruder Johann Mathematik bei – eine Leidenschaft, die beide von klein auf teilten. Sehr zum Leidwesen ihres Vaters, der für seine Söhne eine andere Karriere vorsah. Deshalb ließ er die beiden nicht ihrer Passion nachgehen. Jakob studierte auf Wunsch seiner Eltern Philosophie und Theologie, besuchte aber heimlich Vorlesungen der Mathematik und Astronomie. Auch Johann beugt sich dem Willen seiner Eltern und studiert Medizin, bekam aber immer wieder interessante Mathematikaufgaben von seinem älteren Bruder gestellt. Glücklicherweise konnten beide Ende des 17. Jahrhunderts über Umwege ihren Traum verwirklichen: Jakob forschte an einem Lehrstuhl für Mathematik in Basel, Johann in Groningen.

Anders, als man vielleicht erwarten würde, hat dieser schwierige Lebensweg die beiden Brüder nicht zusammengeschweißt. Im Gegenteil. Zwischen beiden wuchs eine Rivalität heran, die im Lauf der Jahre immer stärker wurde. So forderten sie sich immer wieder gegenseitig durch anspruchsvolle Mathematikaufgaben heraus und machten sich öffentlich über die Fehler des jeweils anderen lustig.

Ein Problem für die brillantesten Köpfe der Welt

Irgendwann hatte Johann Bernoulli genug. Er wollte der Welt sein mathematisches Genie zeigen. Dafür veröffentlichte er im Juni 1696 in der damaligen Fachzeitschrift »Acta eruditorum« das Brachistochronen-Problem, wohl wissend, dass er dieses lösen kann. Die Aufgabe beschäftigt sich mit der Frage, auf welcher Bahn eine Kugel am schnellsten von einem Punkt zu einem niedriger gelegenen Ort rollt.

Er ließ den »brillanten Mathematikern« sechs Monate Zeit zur Lösung dieser Aufgabe. Nach einem halben Jahr hatte ihn jedoch keine einzige richtige Antwort erreicht. Dafür aber ein Brief von Gottfried Wilhelm Leibniz. Er habe zwar innerhalb eines Tages die Differenzialgleichung gefunden, welche die optimale Bewegungsgleichung der Kugel beschreibt. Aber er konnte daraus noch nicht die genaue Form der Bahn ableiten. Er bat um etwas mehr Zeit und legte nahe, dass man die Aufgabe weiter streute, damit mehr Leute die Chance erhielten, sich ihr zu widmen.

Besonders interessant für Leibniz und Bernoulli war das Schweigen Isaac Newtons. Damals war der Prioritätsstreit zwischen Newton und Leibniz bereits losgebrochen: Wer hatte die Differenzial- und Integralrechnung zuerst begründet? Hatte Leibniz von Newton abgeschrieben – oder umgekehrt? Dieser Streit zwischen den beiden Mathematikern nahm bald größere Ausmaße an und es entstand eine Art Konkurrenzkampf zwischen Fachleuten der britischen Insel und des europäischen Festlands.

Großbritannien versus Europa

Newton war inzwischen Mitte 50, hatte sich von seinem Lehrstuhl zurückgezogen und arbeitete in der königlichen Münzprägeanstalt. Leibniz und Bernoulli vermuteten daher, dass er inzwischen einige seiner mathematischen Fähigkeiten eingebüßt hatte und an dem Brachistochronen-Problem gescheitert war.

Die beiden Mathematiker witterten daher die Chance, die mathematische Überlegenheit des europäischen Festlands beweisen zu können. Dazu brauchten sie Lösungen des Brachistochronen-Problems. Bernoulli ließ sich daher überzeugen, es erneut in Umlauf zu bringen und achtete darauf, dass es großflächig verteilt wurde. Zudem verlängerte er die Einsendefrist bis Ostern 1697.

»Ich mag es nicht, von Ausländern wegen mathematischer Dinge belästigt und geneckt zu werden«Isaac Newton, Physiker

Doch der Plan ging nicht auf. Newton hatte nicht geschwiegen, weil er an der Aufgabe gescheitert war, sondern weil er nichts davon mitbekommen hatte. Durch die erneute Ausschreibung erfuhr er von Bernoullis Herausforderung. Er fand die Aufgabe in einem Brief vor, nachdem er gegen 16 Uhr von seiner Arbeit bei der Münzprägeanstalt zurückgekehrt war. »Ich mag es nicht, von Ausländern wegen mathematischer Dinge belästigt und geneckt zu werden«, schrieb er hinterher.

Doch er konnte nicht anders: Er setzte sich sofort ans Werk und verließ seiner Nichte zufolge seinen Schreibtisch erst wieder um 4 Uhr morgens, nachdem er das Brachistochronen-Problem bewältigt hatte. Die Lösung schickte er – wie für Newton typisch ohne den Rechenweg – an Charles Montagu, den damaligen Präsidenten der Royal Society, einer prestigeträchtigen Gelehrtengesellschaft zur Wissenschaftspflege. Montagu veröffentlichte sie daraufhin anonym in den »Transactions of the Royal Society«.

»Ich erkenne einen Löwen an seiner Klaue«Johann Bernoulli, Mathematiker

Das blieb nicht unbemerkt. Als Bernoulli die Lösung sah, erkannte er sofort Newtons unvergleichlichen Stil. »Ich erkenne einen Löwen an seiner Klaue«, schrieb Bernoulli an einen Kollegen. Doch Newton war nicht der Einzige, der das Problem knackte. Tatsächlich reihte sich neben ihm das Who's who der damaligen Mathematik ein: Leibniz, Guillaume de l'Hospital, Ehrenfried Walter Graf von Tschirnhaus und Jakob Bernoulli kamen alle auf das gleiche Ergebnis. Erstaunlicherweise unterschied sich ihre Herangehensweise stark voneinander.

Besonders stachen die Arbeiten der Brüder Bernoulli heraus. Jakob hatte eine Methode entwickelt, die sich auf eine ganze Reihe von Problemen anwenden lässt – nicht nur das der Brachistochrone. Sein Bruder Johann hingegen ließ sich von den Gesetzen der Optik inspirieren. Sein überaus eleganter Ansatz führte letztlich zum »Prinzip der stationären Wirkung«, einem Formalismus, der inzwischen ein Grundpfeiler der Physik ist. »So finden wir in diesen beiden Brüdern die beiden grundlegenden Züge hoher wissenschaftlicher Begabung voneinander getrennt – Züge, die in den allergrößten Naturforschern, in Newton zum Beispiel, vereint sind«, schrieb der Physiker und Philosoph Ernst Mach in seinem 1883 erschienenen Buch »Die Mechanik in ihrer Entwicklung«.

Das mathematische Brachistochronen-Problem

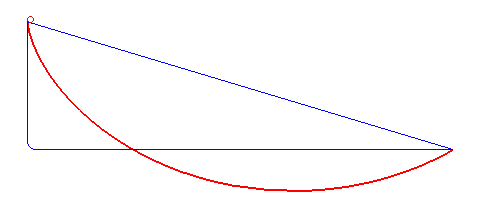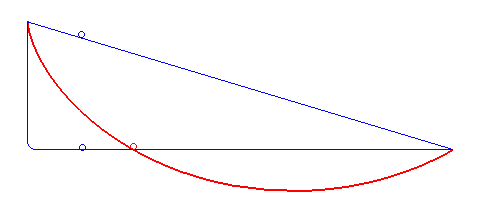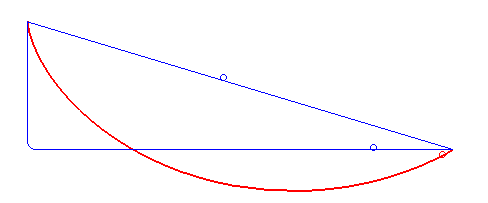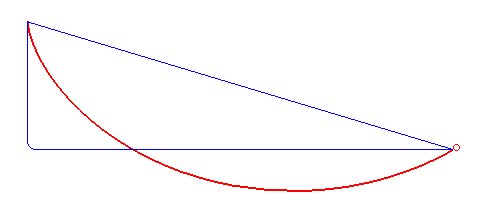
Welche Kurve führt eine Kugel am schnellsten von einem Punkt A zu einem niedriger gelegenen Punkt B? Ein solches Problem lässt sich mit der gewöhnlichen Analysis, wie man sie in der Schule lernt, nicht lösen. Denn hier wird nicht ein einzelner optimaler Wert gesucht (etwa der Scheitelpunkt einer Funktion), sondern eine optimale Kurve, die aus unendlich vielen Punkten besteht.

Dieser Aufgabe hatte sich schon Galileo Galilei 60 Jahre früher gewidmet. Würde man die beiden Punkte A und B durch eine Gerade verbinden, wäre die Strecke minimal. Allerdings ist diese dadurch nicht besonders steil, wodurch die Kugel nicht so stark beschleunigt wird. Deshalb vermutete Galilei, dass ein Kreisbogen die optimale Lösung zum Brachistochronen-Problem liefert. Entlang einer solchen Kurve würde die Kugel demnach am schnellsten den Punkt B erreichen. Wie sich herausstellte, lag er falsch.

Die Bernoullis erkannten, dass die optimale Lösung eine Zykloide ist. Das ist die Kurve, die man erhält, wenn man einen Punkt auf einem Kreis verfolgt, wenn sich dieser auf einer Ebene abrollt. Doch das Entscheidende ist aus heutiger Sicht nicht die Lösung des Problems, sondern der Weg, der sie dahin führte. Vor allem Johann Bernoullis Lösungsweg ist noch heute besonders beeindruckend. Er ließ sich dabei von der Idee der Lichtbrechung inspirieren.

Welchen Weg wählt das Licht?

Der antike Gelehrte Heron von Alexandria hatte schon zu Beginn unserer Zeitrechnung vermutet, dass Licht immer dem kürzesten Pfad folgt. Das erklärt beispielsweise das Reflexionsgesetz, wonach der Einfallswinkel eines Lichtstrahls dem Ausgangswinkel entspricht – denn so beschreitet Licht den kürzesten Weg durch den Raum. Doch das erklärt nicht das Phänomen der Lichtbrechung, etwa wenn ein Lichtstrahl in Wasser oder ein anderes Medium eindringt.

Pierre de Fermat erkannte 1662, dass Licht nicht den kürzesten Weg nimmt, sondern den schnellsten. Anstatt die Strecke zu verkleinern, minimieren die Strahlen offenbar die Zeit. Da die Lichtgeschwindigkeit in einem optisch dichteren Medium abnimmt, erklärt dieses »fermatsche Prinzip« die Winkeländerung, die sich durch das snelliussche Brechungsgesetz berechnet.

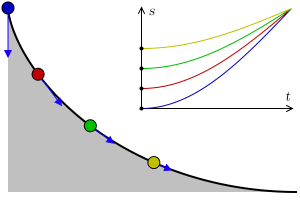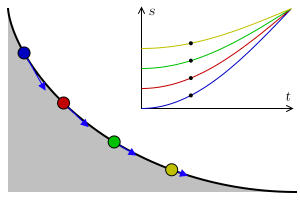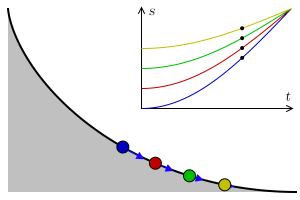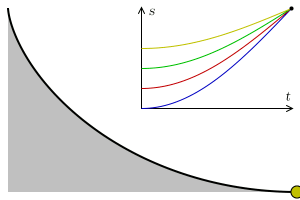
Johann Bernoulli nahm das als Ausgangspunkt, um das Brachistochronen-Problem zu lösen. In diesem Fall übernimmt die Kugel die Rolle des Lichts. Denn auch ihre Geschwindigkeit ändert sich – allerdings nicht an einer Grenzfläche, sondern an jedem Punkt im Raum. Die Kugel wird durch die Schwerkraft immer schneller. Man kann sich also vorstellen, dass der Raum von unendlich vielen waagrechten Linien durchzogen ist, die jeweils eine Art Grenzfläche darstellen. An jeder dieser Linien folgt die Kugel dem snelliusschen Brechungsgesetz – und minimiert so die Zeit, die sie von A nach B braucht.

Indem er den Grenzwert unendlich vieler solcher horizontaler Linien berechnete, konnte Johann Bernoulli die optimale Bahnkurve bestimmen. Er erkannte, dass die Kugel dem Weg einer Zykloide folgt. Diese Kurve bildet den besten Kompromiss aus kurzem Weg einerseits und steilem Abstieg andererseits. Besonders interessant ist hierbei, dass es völlig egal ist, an welcher Stelle der Zykloide ein Ball startet: Er wird den Endpunkt B immer zur gleichen Zeit erreichen.

Ein universelles Prinzip der Natur

Zu dieser Zeit war noch nicht klar, welche enormen Auswirkungen Johann Bernoullis Berechnungen haben würden. Der 1698 geborene Mathematiker Pierre Louis Moreau de Maupertuis griff diese Idee Jahre später auf und verallgemeinerte sie: Warum sollte nur Licht dem fermatschen Prinzip folgen? Vielleicht ist es eine allgemeine Eigenschaft der Natur. Während Maupertuis seinerzeit für die Idee belächelt wurde, entwickelten William Rowan Hamilton und Joseph Louis Lagrange daraus Ende des 18. Jahrhunderts das berühmte »Prinzip der stationären Wirkung«, das durch die Formel δS = 0 ausgedrückt wird.

Demnach laufen alle natürlichen Prozesse stets so ab, dass sie die »Wirkung« S minimieren (oder maximieren). Möchte man zum Beispiel beschreiben, welcher Flugbahn ein Ball folgt, den ich in die Luft werfe, muss man nur das Prinzip der stationären Wirkung anwenden. Klar, man könnte auch – wie man es in der Schule lernt – die Kräfte heranziehen, die auf den Ball wirken (die von mir aufgebrachte Kraft beim Wurf sowie die Schwerkraft, die ihn nach unten zieht, und wenn man ganz genau ist auch den Luftwiderstand). Viel direkter ist jedoch der Ansatz mit der Wirkung: Man setzt dort nur ein paar Werte ein, macht zwei bis drei Umformungen und tada! schon hat man die Bewegungsgleichung des Balls da stehen, ohne lange darüber nachdenken zu müssen, in welche Richtung welche Kraft wirkt und wie man sie richtig miteinander verrechnet.

Aber was ist diese ominöse Wirkung? Im einfachsten Fall handelt es sich dabei um die kinetische Energie minus der potenziellen. Im Fall eines geworfenen Balls also die Bewegungsenergie minus der Lageenergie. Das Prinzip der stationären Wirkung gibt an, wie man mit dieser Differenz rechnen muss, um dann die Bewegungsgleichung des Balls zu erhalten. Das Erstaunliche ist: Das Prinzip gilt nicht nur für die Mechanik, sondern auch für die Quantenmechanik, die Teilchenphysik und für die allgemeine Relativitätstheorie. Völlig egal, was man beschreiben möchte – ob Bälle, Quarks, Galaxien oder die Raumzeit an sich –, alles scheint dem Prinzip der stationären Wirkung zu folgen.

Damit hatte Johann Bernoulli seinen gewünschten Erfolg. Doch sein Bruder Jakob legte ebenfalls eine beeindruckende Lösung des Brachistochronen-Problems vor. Und kaum war dieser Wettstreit beendet, forderte Jakob seinen jüngeren Bruder öffentlich heraus: Welche geschlossene Kurve hat gemessen an ihrem Umfang den größten Flächeninhalt? Wie zu erwarten, verbesserte das die Beziehung der beiden nicht, sondern mündete in einen fiesen Streit, den sie öffentlich austrugen …