Lexikon der Chemie: Normierungsbedingung
Normierungsbedingung, in der Quantenmechanik die Forderung an die Wellenfunktion Ψ(x,y,z), daß die Integration ihres Betragsquadrates |Ψ|2 = Ψ*(x,y,z) Ψ(x,y,z) über den gesamten Raum den Wert 1 ergeben muß (quantenmechanisches Atom-Modell). Die N. ist eine Folge der statistischen Interpretation der Wellenfunktion, wonach |Ψ|2 die Wahrscheinlichkeitsdichte darstellt. Die N. wird meist in der Form angegeben:
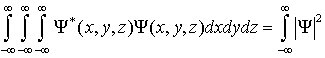
.
Erfüllt eine Wellenfunktion φ(x,y,z) nicht die N., so erhält man die normierte Wellenfunktion aus der Gleichung Ψ(x,y,z) = A-1/2 φ(x,y,z), wobei A-1/2 den Normierungsfaktor bezeichnet. Normierbar sind nur eindeutige, stetige, endliche Wellenfunktionen.
Copyright 1998 Spektrum Akademischer Verlag, Heidelberg
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.