Hemmes mathematische Rätsel: Das rollende Dreieck
Darryl Francis wurde 1948 geboren und hat viele Bücher über das Brettspiel »Scrabble« geschrieben. Er hat unzählige Wörterspiele und -rätsel entworfen, aber auch einige mathematische Knobeleien. 1974 veröffentlichte er in der Zeitschrift »Games and Puzzles« folgendes Rätsel:
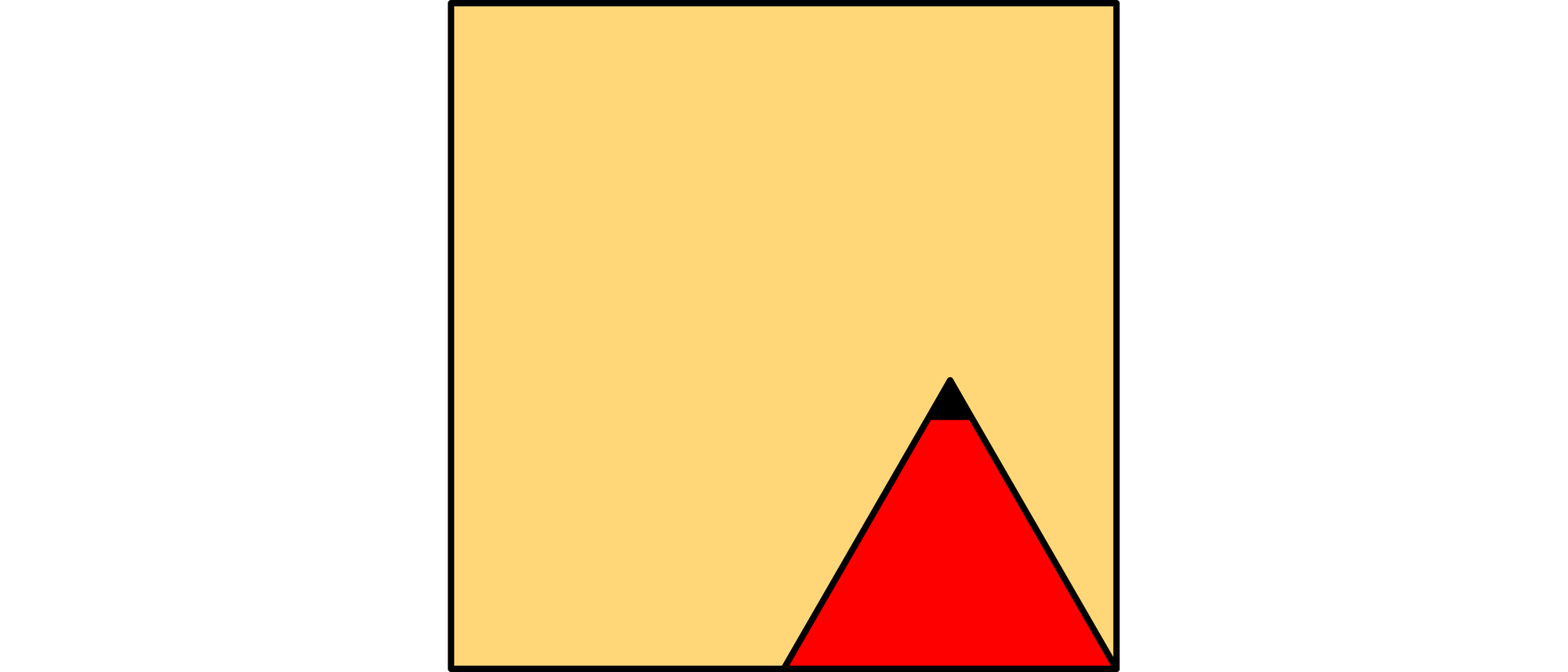
Im Inneren eines Quadrates von 20 cm Seitenlänge liegt, so wie es die Skizze zeigt, ein gleichseitiges Dreieck von 10 cm Seitenlänge. Eine Ecke des Dreiecks ist schwarz markiert. Das Dreieck wird nun im Uhrzeigersinn auf den Innenseiten des Quadrates abgerollt. Wie lang ist der Weg der schwarzen Spitze, wenn das Dreieck so weit gerollt wird, bis es sich wieder in seiner Ausgangsposition befindet und die schwarze Spitze wieder nach oben zeigt?
Der Umfang des Quadrates ist achtmal so lang wie eine Dreiecksseite. Nach acht Abrollungen befindet sich das Dreieck also wieder in seiner Ausgangsstellung. Nach jeder dritten Abrollung ragt die schwarze Ecke ins Innere des Quadrates, ansonsten liegt sie an seinem Umfang. Da 8 nicht durch 3 teilbar ist, zeigt die schwarze Spitze nicht nach oben, wenn das Dreieck die Ausgangsstellung erreicht hat. Erst nach drei kompletten Umläufen durch das Quadrat hat die schwarze Spitze wieder ihre ursprüngliche Position erreicht.
Das Dreieck macht beim Rollen immer abwechselnd zwei verschiedene Bewegungen: eine Drehung um 120° und eine Drehung um 30° jeweils um seine vordere Ecke. Bei 24 Abrollungen dreht sich das Dreieck also insgesamt 1800°, was fünf vollständigen Umdrehungen entspricht. Die schwarze Ecke macht nur zwei Drittel der Drehungen mit; bei einem Drittel ist sie der Drehpunkt. Das bedeutet, die schwarze Ecke dreht sich nur 10/3-mal im Kreis. Da die Seiten a des Dreiecks die Radien der Drehkreise sind, hat der gesamte Weg der schwarzen Ecke die Länge 10/3 · 2 · π · a ≈ 209,44 cm.
Schreiben Sie uns!
Beitrag schreiben