Hemmes mathematische Rätsel: Welcher Wert ist gesucht?
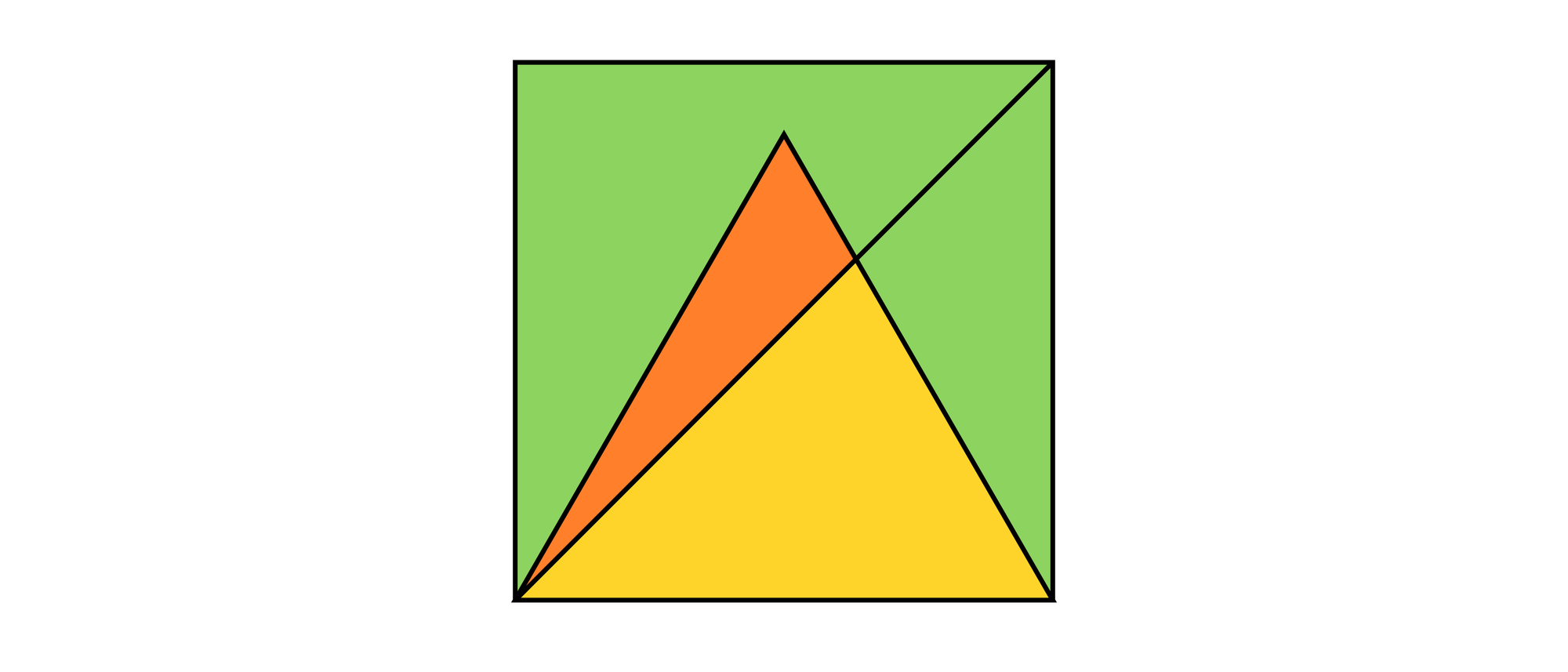
Ein Quadrat und ein gleichseitiges Dreieck überlappen sich und haben eine Grundseite der Länge 1 gemeinsam. Eine Diagonale des Quadrates schneidet von dem Dreieck das orangefarbene Stück ab. Welchen Flächeninhalt hat das abgeschnittene Stück?
Die Höhe eines gleichseitigen Dreiecks ist das 1/2√3-Fache seiner Seitenlänge. Da das Dreieck ABE die Seitenlänge 1 hat, ist die Länge seiner Höhe h = 1/2√3 und der Inhalt seiner Fläche X = 1/4√3. Das Dreieck BGH ist die rechte Hälfte eines gleichseitigen Dreiecks der Seitenlänge a. Folglich hat seine Grundseite HB die Länge a/2 und seine Höhe GH die Länge k = 1/2√3 · a. Das Dreieck AHG ist rechtwinklig und gleichschenklig, und darum haben seine beiden Katheten AH und GH die Länge k. Somit gilt für die untere Seite AB des Quadrates k + a/2 = 1, was man zu a = 2(1 – k) umformen kann. Dies wird in die Höhengleichung eingesetzt und ergibt k = 1/2√3 · 2(1 – k) oder k = 1/2(3 – √3). Das Dreieck ABG hat den Flächeninhalt Y = 1/2k = 1/4(3 – √3). Die Fläche des orangefarbenen Dreiecks AGE ist die Differenz der Flächen der Dreiecke ABE und ABG und hat damit den Wert X – Y = 1/4√3 – 1/4(3 – √3) = 1/4(2√3 – 3) ≈ 0,116.
Schreiben Sie uns!
Beitrag schreiben