Hemmes mathematische Rätsel: Den wievielten Teil der gesamten Sternfläche nimmt das Achteck ein?
Zwei gleiche Rhomben, deren lange Diagonalen doppelt so lang sind wie ihre kurzen, werden so übereinandergelegt, dass sich ihre langen Diagonalen mittig und rechtwinklig kreuzen. Dabei entsteht ein vierzackiger Stern mit einem gleichseitigen Achteck im Inneren.
© Heinrich Hemme (Ausschnitt)
2020 veröffentlichte Reiner Ketteniß aus Eschweiler in den »Aachener Nachrichten« und in der »Aachener Zeitung« ein geometrisches Problem.
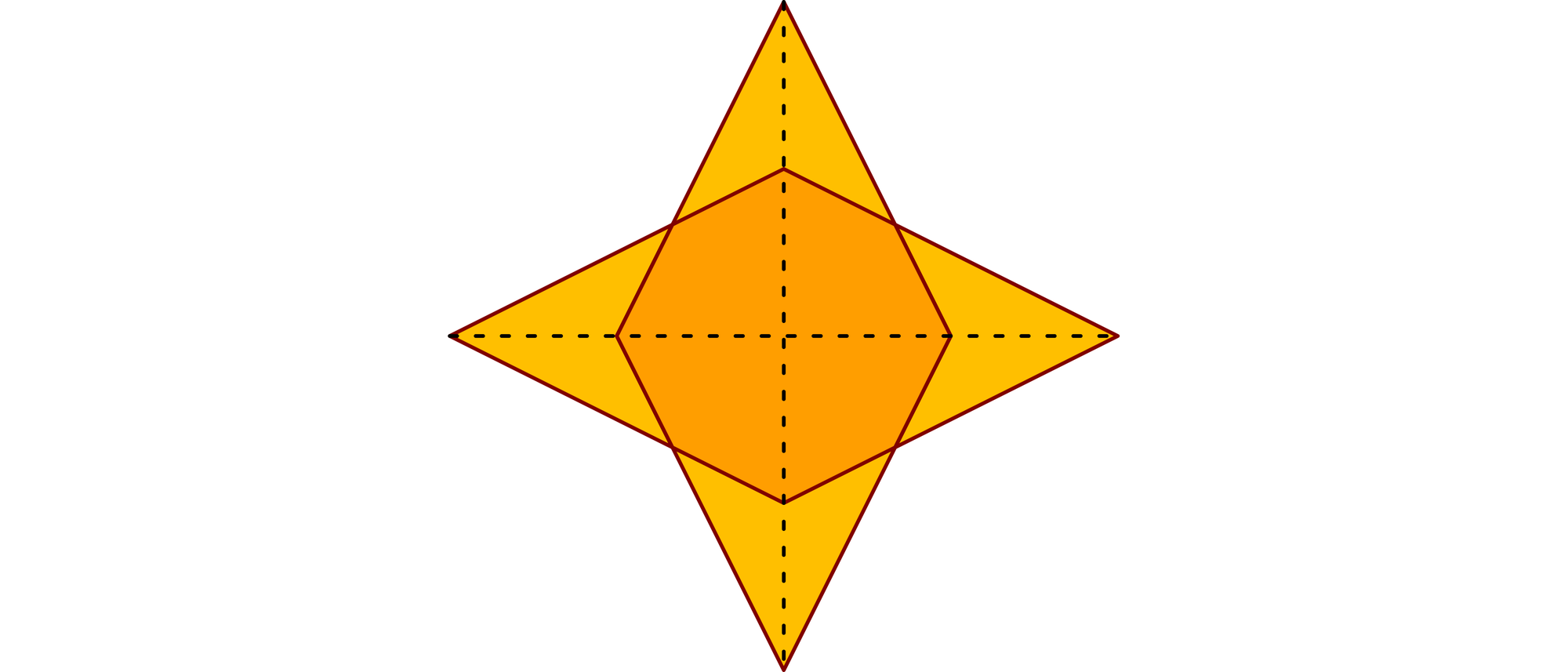
Zwei gleiche Rhomben, deren lange Diagonalen doppelt so lang sind wie ihre kurzen, werden so übereinandergelegt, dass sich ihre langen Diagonalen mittig und rechtwinklig kreuzen. Dabei entsteht ein vierzackiger Stern mit einem gleichseitigen Achteck im Inneren.
Den wievielten Teil der gesamten Sternfläche nimmt das Achteck ein?
Wegen der Symmetrie des Sterns reicht es aus, nur ein Achtel von ihm zu betrachten. Das orange und das rote Dreieck haben dieselbe Höhe und gleich lange Grundseiten und somit den gleichen Flächeninhalt. Das Achteck nimmt also genau die Hälfte der Sternfläche ein.
© Heinrich Hemme
Schreiben Sie uns!
Beitrag schreiben