Hemmes mathematische Rätsel: Wie groß ist das Landstück des Bauern?
Der Mathematiker Achim Roth wurde 1955 in Köln geboren. Er studierte in Bonn und lebt in Frankfurt am Main. Im Januar 2022 schickte er mir ein hübsches Problem aus der ebenen Geometrie, das er selbst entwickelt hatte.
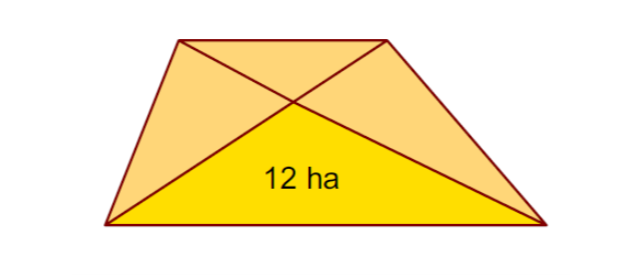
Ein Bauer stirbt und hinterlässt seinen vier Söhnen ein trapezförmiges Landstück. In seinem Testament hat er bestimmt, dass es durch die beiden Diagonalen in vier Stücke geteilt werden muss und sein ältester Sohn das größte Stück von 12 Hektar erhalten soll. Wie groß ist das gesamte Landstück, wenn die Diagonalen sich gegenseitig im Verhältnis 2 : 1 scheiden?
Die Verhältnisse der Diagonalenabschnitte betragen SC/AS = SD/BS = 1/2. Nach dem Strahlensatz gilt dies auch für die Höhen- und Grundseitenverhältnisse der beiden Dreiecke ABS und CDS. Somit ist k/h = b/a = 1/2 oder k = h/2 und b = a/2. Der Inhalt der Trapezfläche beträgt (h + k)(a + b)/2 = (h + h/2)(a + b/2)/2 = 9/4 · ah/2. Da das Dreieck ABS den Flächeninhalt 12 hat, beträgt der Inhalt des gesamten Trapezes 9/4 · 12 = 27. Der Bauer hat seinen Söhnen somit 27 Hektar Land vermacht.
Schreiben Sie uns!
3 Beiträge anzeigen