Hemmes mathematische Rätsel: Wie groß ist der Flächeninhalt der Quadrate?

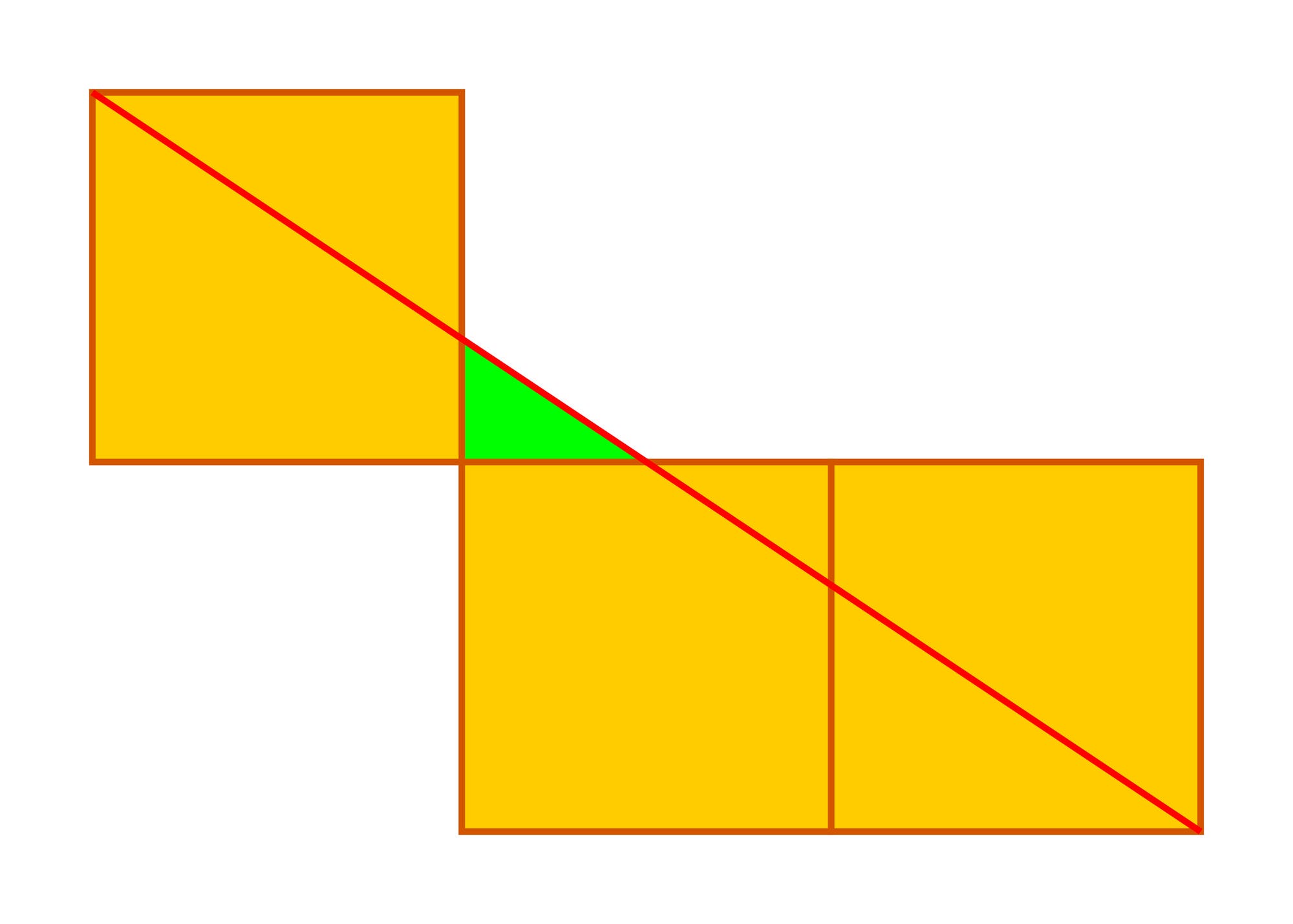
Die obere linke und die untere rechte Ecke einer Figur aus drei gleichen aneinanderhängenden Quadraten sind durch eine gerade Linie miteinander verbunden. Das grüne Dreieck, das dabei entsteht, hat einen Flächeninhalt von 1. Wie groß ist der Flächeninhalt jedes der drei Quadrate?
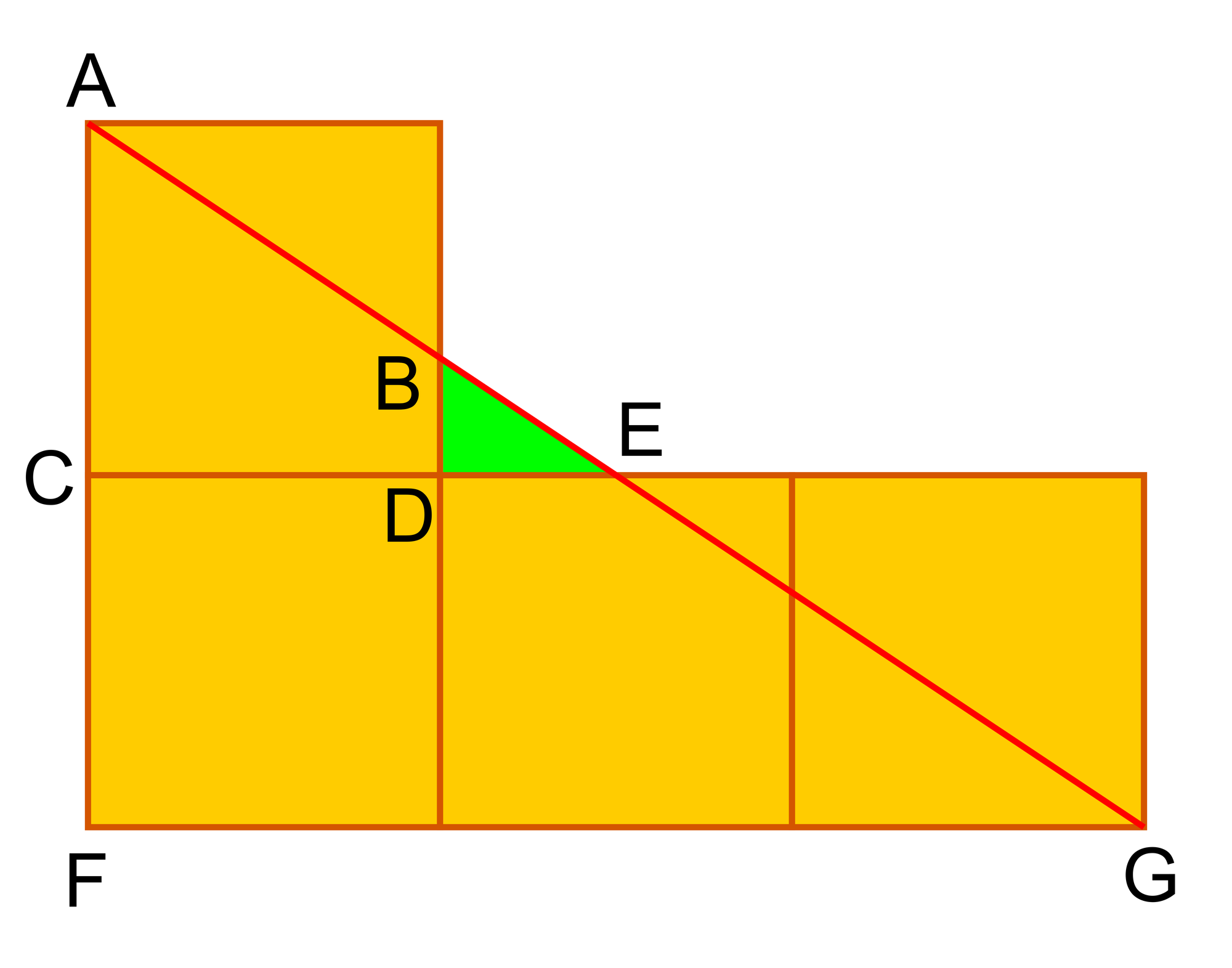
Wir ergänzen die Zeichnung noch um ein viertes Quadrat, das wie die drei anderen Quadrate die Seitenlänge a hat. Die beiden Dreiecke ACE und AFG sind ähnlich. Darum gilt für die Kathetenverhältnisse CE/AC = FG/AF oder CE/a = 3a/(2a), was man zu CE = 3a/2 umformen kann. Außerdem gilt DE = CE – CD oder DE = 3a/2 – a = a/2. Auch die beiden Dreiecke BDE, und ACE sind ähnlich. Darum gilt für die Kathetenverhältnisse BD/DE = AC/CE oder BD/(a/2) = a/(3a/2), was sich zu BD = a/3 umstellen lässt. Das grüne Dreieck hat den Flächeninhalt 1/2 · BD · DE = 1 oder 1/2 · a/3 · a/2 = 1, woraus sich als Flächeninhalt der einzelnen Quadrate a2 = 12 ergibt.






Schreiben Sie uns!
4 Beiträge anzeigen