Keplersche Gesetze: Wie konnte Johannes Kepler sein 3. Gesetz herleiten?
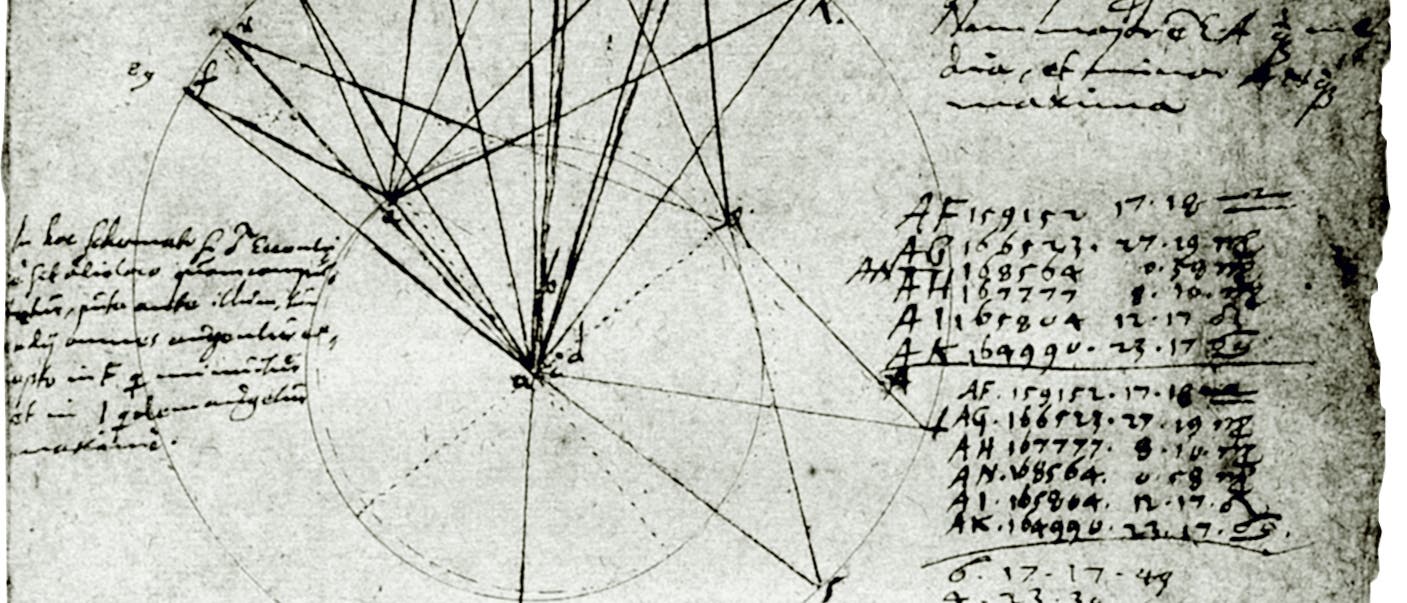
(Horst Gers, Meschede)
Aus den zu einer Vielzahl von Zeitpunkten beobachteten Positionen errechnete Kepler die jeweiligen Winkel zwischen Sonne, Erde und Mars. So konnte er mittels Triangulation die wahren Bahnen von Erde und Mars rekonstruieren.
Keplers Aufzeichnungen enthalten zahlreiche Abbildungen für dieses Vorgehen. Indem Kepler den Umstand nutzte, dass Mars alle 687 Tage (dies ist seine siderische Umlaufzeit) an der gleichen Stelle seiner Bahn steht, die Erde dann aber an verschiedenen Positionen ihrer Bahn, konnte er die Bahnellipse der Erde mit all ihren Parametern bestimmen. Dazu gehören die Exzentrizität, der größte und der kleinste Abstand von der Sonne (das Aphel und das Perihel) sowie die Lage der Apsidenlinie, die durch diese beiden Bahnpunkte geht.
Nach der Charakterisierung der Erdbahn konnte Kepler auch die Umlaufbahn des Mars bestimmen, indem er nun die Triangulation für verschiedene Punkte der Marsbahn ausführte. Für diese kamen noch weitere Bahnelemente hinzu: ihre Neigung gegenüber der Erdbahnebene und die Schnittlinie beider Ebenen, die durch einen aufsteigenden und einen absteigenden Knoten auf der Bahn definiert ist. Alle Abstände gab er als Verhältniswerte zur großen Halbachse der Erde an. Auf diese Weise ließ sich schließlich eine Landkarte des Sonnensystems mit den Bahnen aller Planeten erstellen – wenn auch nur im relativen Maßstab.
Die Opposition des Mars im Oktober 2020 bot unseren Lesern Gelegenheit, seine große Halbachse näherungsweise selbst zu ermitteln. Denn nun lagen Erde und Mars pro Zeiteinheit parallele Bahnstücke zurück. Deren Länge ist gegeben durch ωE · rE und ωM · rM, wobei ω die im Bogenmaß ausgedrückte Winkelgeschwindigkeit (360°/365 Tage beziehungsweise 360°/687 Tage) und r die große Halbachse ist. Der Mars bleibt um das Stück R auf seiner Bahn gegenüber der Erde zurück. Ein Beobachter auf der Erde sieht dieses Stück unter einem Winkel, der (pro Zeiteinheit) die Winkelgeschwindigkeit ωR der rückläufigen Bewegung in der Oppositionsschleife ist. Mit den aus der Skizze abzulesenden Beziehungen
$$ω_{R} = \frac{R}{r_{M} – r_{E}} \text{ und } R = ω_{E} \cdot r_{E} – ω_{M} \cdot r_{M}$$ergibt sich
$$r_{M} = r_{E} \cdot \frac{(ω_{R} + ω_{E})}{(ω_{R} + ω_{M})}.$$Probieren Sie es aus!
(Max Bauer, Hildesheim)
Die siderische Umlaufzeit ist die Zeit, welche ein Planet auf seiner wahren Bahn für einen vollständigen Umlauf um die Sonne braucht. Von der Sonne aus gesehen, steht er nach einem Umlauf wieder vor dem genau gleichen Sternenhintergrund. Das Problem: Die siderische Umlaufzeit lässt sich nur für die Erde direkt bestimmen, für alle anderen Planeten muss sie errechnet werden. Denn ein Beobachter auf der Erde sieht nicht deren wahre, sondern nur ihre scheinbaren Bahnen. Direkt messen kann er nur die Zeit, die zum Beispiel für einen oberen Planeten wie den Mars zwischen einer Opposition und der nächsten vergeht. Diese gemessene synodische Umlaufzeit gibt die Zeitspanne an, nach der ein Planet von der Erde aus gesehen wieder im gleichen Winkel zur Sonne steht. Für die mit freiem Auge sichtbaren Planeten waren die synodischen Umlaufzeiten schon seit dem Altertum recht gut bekannt, und in den langjährigen Aufzeichnungen von Tycho Brahe fand Kepler sie mit besonders hoher Genauigkeit.
Für die Berechnung greifen wir wieder auf die obige Grafik zurück. Um die Zeit seiner Opposition herum bewegen sich der Mars und die Erde auf parallelen Bahnstücken – Mars mit etwas geringerer, die Erde mit etwas höherer Winkelgeschwindigkeit. Die Winkelgeschwindigkeit ω eines Planeten mit der siderischen Umlaufzeit T beträgt ω = 360°/T (weil nach einer siderischen Umlaufzeit ein Vollkreis beschrieben wird). Für die Erde schreiben wir ωE = 360°/TErde, für den Mars, den wir als Beispiel eines oberen Planeten nehmen, ωM = 360°/TMars. Die Differenz ωE − ωM dieser beiden Winkelgeschwindigkeiten ist der Vorsprung, den die Erde pro Zeiteinheit gegenüber dem Mars herausholt. Nach einer synodischen Umlaufzeit UMars, nach der es wieder zur Opposition kommt, muss dieser Vorsprung auf volle 360 Grad angewachsen sein. Deshalb gilt also:
$$(ω_{E}-ω_{M}) \cdot U_{Mars} = 360°$$Setzen wir in diese Gleichung die genannten Beziehungen für ωE und ωM ein und formen etwas um, erhalten wir für die siderische Umlaufzeit TMars des Mars die Formel:
$$T_{Mars} = \frac{(U_{Mars} \cdot T_{Erde})}{(U_{Mars} – T_{Erde})}.$$Hierbei haben wir stillschweigend als Vereinfachung angenommen, dass die Planetenbahnen Kreise und nicht gegen die Ekliptik geneigt sind und dass sich die Planeten mit konstanter Geschwindigkeit auf diesen Kreisbahnen bewegen. Diese Näherung ist gerechtfertigt, aber Kepler erkannte gerade in den nicht wegzudiskutierenden Abweichungen, die er in Brahes genauen Beobachtungsdaten fand, dass sich die Planeten innerhalb eines siderischen Umlaufs mit wechselnder Geschwindigkeit und auf Ellipsenbahnen bewegen.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.