Als man früher versuchte, die Bewegung der Himmelskörper zu verstehen, benutzte man dazu lange Zeit Epizykeln. Eigentlich hätte man ja gerne gehabt, dass sich Sonne, Mond und Planeten alle auf exakten Kreisbahnen um die Erde herumbewegen. Das wäre schön ordentlich und ästhetisch ansprechend gewesen, passte aber leider nicht zur beobachteten Realität. Also dachte man sich eben eine Bewegung entlang eines Kreises, der einen weiteren Kreis um die Erde herum entlangwandert. Auch das passte nicht; man musste immer weiter an der Konfiguration der Kreise herumbasteln, bis Johannes Kepler endlich zeigen konnte, dass man auf die Erde im Mittelpunkt verzichten und gleichzeitig die Kreise vergessen muss. Man braucht elliptische Bahnen um die Sonne herum, dann passt alles wunderbar.

Das war das endgültige Ende der Epizykeltheorie; in der Mathematik lässt man aber immer noch gerne Kreise auf anderen Kreisen herumrollen. Und bekommt dabei Formeln wie diese hier:

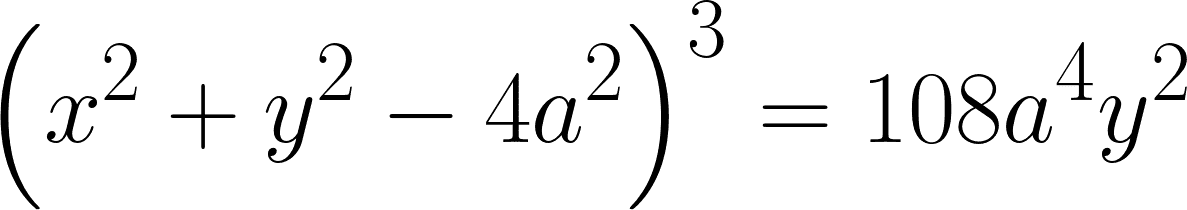
Diese Gleichung ist die implizite Darstellung einer Nephroide. Das ist die Kurve, die ein Punkt auf einem kleinen Kreis mit Radius a beschreibt, wenn er entlang eines größeren Kreises mit Radius 2a abrollt, dessen Mittelpunkt sich genau im Ursprung eines Koordinatensystems befindet. Der Namen bezieht sich auf die nierenförmige Gestalt der Kurve. Mathematisch kann man mit einer Nephroide jede Menge interessante Sachen anstellen.

Wenn man aufmerksam genug ist, kann man eine Nephroide aber auch im Alltag beobachten. Zumindest teilweise, zum Beispiel in der Kaffeetasse. Ihre Innenseite ist eine gebogene Fläche und typischerweise kann das Material, aus der die Tasse besteht, Licht gut spiegeln. Wenn Lichtstrahlen schräg auf die Innenseite der Tasse fallen, werden sie dort reflektiert. Auf der Oberfläche des Kaffees – sofern noch nicht ausgetrunken – sieht man dann einen leuchtenden Bereich, der den Teil einer Nephroide bildet.

Wie im Schwimmbad, so auch im Weltall

Das liegt daran, dass es nicht einfach ist, ein Bündel paralleler Lichtstrahlen wirklich exakt in einen einzigen Punkt zu reflektieren. Dort, wo sich die durch die gebogene Fläche unterschiedlich abgelenkten Lichtstrahlen überlagern, erhält man eine Brennfläche beziehungsweise Brennlinie. Diesen Effekt nennt man Kaustik – und bei einem halbwegs regelmäßig geformten Objekt wie einer Kaffeetasse ist sie durch eine entsprechend regelmäßige mathematische Struktur wie eben eine Nephroide beschreibbar. Kaustiken findet man aber auch in vielen anderen Fällen. Die typischen Lichtreflexionen am Boden eines Schwimmbads etwa werden auf die gleiche Weise gebildet – in diesem Fall durch Brechung statt Reflexion –, sind aber auf Grund der Bewegung des Wassers deutlich unregelmäßiger.

Kaustiken spielen in der Astronomie ebenfalls eine wichtige Rolle, selbst dort, wo es nicht um die Optik von Linsen und Spiegeln der Teleskope geht. Der Weg von Lichtstrahlen lässt sich nicht nur durch optische Bauteile verändern, sondern auch durch die Anwesenheit großer Massen. Kommt etwa das Licht einer fernen Galaxie an einer etwas näher gelegenen Galaxie vorbei, dann sorgt die Krümmung der Raumzeit durch diese große Masse dafür, dass die Lichtstrahlen abgelenkt und Objekte vergrößert sichtbar werden.

Man nennt so etwas Gravitationslinse, und dieser Effekt erlaubt es der Astronomie, Dinge zu sehen, die ansonsten kaum sichtbar wären. Ganz besonders gilt das, wenn die Massen im All zufällig so angeordnet sind, dass sich Objekte genau auf der Kaustik befinden; entlang der Linie, wo der Vergrößerungseffekt maximal ist.

Mit etwas Glück kann die Astronomie solche Konfigurationen nutzen, um Einzelsterne sichtbar zu machen, die so weit entfernt sind, dass normale Teleskope keine Chancen hätten, sie zu sehen. Und vielleicht kann man so auch irgendwann einen Blick auf die allerersten (und damit entferntesten) Sterne des Kosmos werfen.