Nicht bloß in der weihnachtlichen Folklore, sondern fraglos auch aus mathematischer Sicht hat die 24 einiges zu bieten.

Betrachten wir dazu diese Formel:

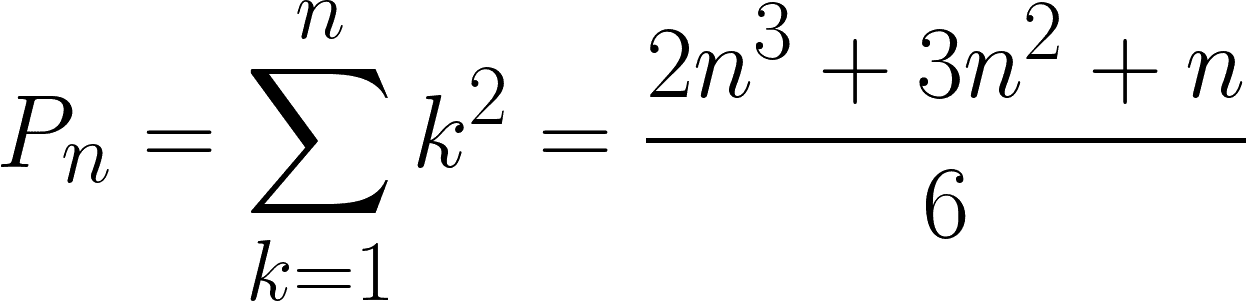
Damit werden so genannte quadratische Pyramidenzahlen beschrieben. Die kann man sich durchaus bildlich vorstellen: Angenommen, man hat einen Haufen Kugeln (es müssen nicht zwingend Kugeln für den Weihnachtsbaum sein) und möchte sie zu einer Pyramide mit quadratischer Grundfläche stapeln, ergibt die Formel genau die Zahlen, mit denen das möglich ist. Setzt man für die Höhe n = 1, ergibt sich der triviale Fall einer »Pyramide«, die aus genau einer Kugel besteht. Für n = 2 berechnet sich die zweite quadratische Pyramidenzahl zu 5, was eine Struktur beschreibt, in der vier Kugeln ein Quadrat bilden, auf dem oben in der Mitte die fünfte Kugel liegt. Für n = 3 startet man mit einer Basis aus 3 x 3 = 9 Kugeln, auf die eine zweite Schicht mit 2 x 2 = 4 Kugeln gesetzt wird, auf denen dann eine letzte Kugel die Spitze bildet, womit man bei einer quadratischen Pyramidenzahl von 14 landet.

Die Reihe 1, 5, 14 setzt sich mit den Zahlen 30, 55, 91, 140, 204, 285, 385, 506, … fort (wobei manchmal auch die 0 für den Fall n = 0 ganz an den Anfang gesetzt wird). In den simplen Pyramidenzahlen steckt aber mehr, als auf den ersten Blick zu sehen ist. Man kann zum Beispiel fragen, welche der quadratischen Pyramidenzahlen gleichzeitig Quadratzahlen sind. Oder anders gesagt: Welche Anzahl an Kugeln kann man sowohl in einem Quadrat anordnen als auch in einer Pyramide mit quadratischer Grundfläche? Das ist als »Kanonenkugel-Problem« bekannt. Es wurde schon im 16. Jahrhundert diskutiert.

Etwas mathematischer formuliert geht es also um die Frage, welche positiven ganzen Zahlen n und m die Gleichung 1²+2²+ … +n² = m² lösen. Dass dies für den trivialen Fall von n = m = 1 zutrifft, ist offensichtlich. Doch gibt es noch andere Zahlen? Der französische Mathematiker Édouard Lucas hat im Jahr 1875 die Vermutung aufgestellt, das sei lediglich noch für n = 24 (und m = 70) der Fall. Die 24. quadratische Pyramidenzahl lässt sich aus der obigen Formel leicht zu 4900 berechnen, was in der Tat das Quadrat von 70 ist.

Lucas wollte allerdings nicht nur auf eine weitere Lösung hinweisen, sondern hat behauptet, es gebe neben den Paaren (1,1) und (24,70) keine weiteren positiven und ganzen Zahlen mehr, die die Gleichung erfüllen. Das konnte aber erst mehr als vier Jahrzehnte später der englische Mathematiker George Neville Watson beweisen.

Die Zahl 24 ist demnach tatsächlich die einzige nichttriviale Lösung des Kanonenkugel-Problems. Das kann man sich gerne merken, um damit auf Weihnachtsfeiern die Stimmung zu heben (und Feiern, bei denen man die Stimmung mit mathematischen Informationen nicht heben kann, sollte man am besten gar nicht erst besuchen!). Es handelt sich jedoch um mehr als eine reine Kuriosität; diese spezielle Eigenschaft der Zahl 24 spielt eine Rolle in der so genannten bosonischen Stringtheorie, die ursprüngliche Form der Stringtheorie, mit der ab den 1960er Jahren versucht wurde, die Welt der Elementarteilchen und der zwischen ihnen wirkenden Kräfte zu beschreiben.

Die hatte aber nicht nur das Problem, dass sie bloß in einem Raum mit 25 Dimensionen funktioniert, sondern auch jede Menge andere Schwierigkeiten. Moderne Stringtheorien kommen mit weniger Dimensionen aus, brauchen jedoch immer noch mehr als die üblichen drei und müssen sich daneben mit einem Mangel an experimenteller Belegbarkeit herumärgern. Wer zufällig einmal auf die Weihnachtsfeier eines Instituts für Theoretische Physik gerät, sollte die Mathematik der Zahl 24 also vielleicht besser doch nicht erwähnen.