Die Mathematik hat einen großen Vorrat an Symbolen, mit denen sie sich ausdrücken kann. Das kann verwirrend sein, wenn man das Vokabular nicht beherrscht. Mit ein wenig Kreativität reichen aber auch zwei Zahlen, um zu verblüffen. So wie in dieser Formel:

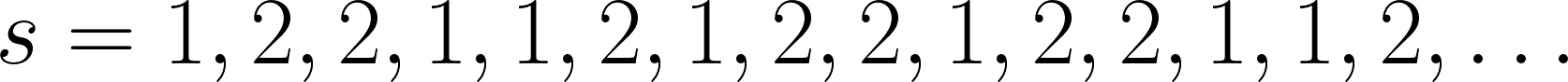
Wenn man diese Folge von Zahlen betrachtet, fällt sofort auf, dass es sich nur um die Ziffern 1 und 2 handelt. Auffällig ist ebenfalls, dass die Ziffern nur alleine oder zu zweit auftauchen. Um zu sehen, wie die Abfolge der Einsen und Zweien zu Stande kommt, muss man aber ein wenig länger nachdenken. Mathematisch exakt ausgedrückt handelt es sich um eine Abfolge von Lauflängen, die gleichzeitig ihre eigene Lauflängenkodierung ist. Etwas verständlicher funktioniert das Ganze so: Wenn wir abzählen, wie oft sich die einzelnen Ziffern wiederholen, und das Ergebnis aufschreiben, ist die resultierende Folge identisch mit der Folge, deren Elemente wir abgezählt haben.

Der erste Block besteht aus der einzelnen Ziffer 1, hat also eine Lauflänge von 1. Der zweite Block – die Wiederholung der Ziffer 2 – hat eine Lauflänge von 2. Dann kommt ein Block mit zwei Einsen, der also ebenfalls eine Lauflänge von 2 hat. Es folgt eine einzelne 2, also ein Block mit einer Lauflänge von 1 und so weiter. Wenn wir die Abfolge der bis jetzt so ermittelten Lauflängen aufschreiben, lautet das Resultat 1, 2, 2, 1. Das entspricht exakt dem Anfang der Ursprungssequenz. Man kann sich leicht davon überzeugen, dass eine Auswertung der Lauflängen tatsächlich die komplette Folge reproduziert.

Zudem ist es möglich, die Folge direkt aus sich selbst zu konstruieren. Dazu gibt man die ersten drei Werte der Sequenz vor: 1, 2, 2. Die letzte 2 in dieser Startsequenz besagt, es müsse nun ein Block mit der Lauflänge 2 folgen; es muss also mit 1, 1 weitergehen. Diese beiden neuen Zahlen in der Folge wiederum bestimmen, dass nun zwei Blöcke mit je einer Lauflänge von 1 kommen sollten. Man hängt also eine 2 und eine 1 an die Sequenz an, was zur Folge 1, 2, 2, 1, 1, 2, 1 führt. Anschließend muss ein Block mit Lauflänge 2, gefolgt von einem mit der Lauflänge 1, kommen: 1, 2, 2, 1, 1, 2, 1, 2, 2, 1. Das lässt sich beliebig fortsetzen.

Ist die Kolakoski-Sequenz periodisch?

Wegen all der Einsen und Zweien könnte man rasch den Überblick verlieren, aber eigentlich ist es leicht, die seltsame Folge aufzuschreiben. Das erste Mal hat das der amerikanische Mathematiker Rufus Oldenburger im Jahr 1939 getan, allerdings in einem sehr speziellen Kontext der symbolischen Dynamik, der nicht dazu geeignet war, die Aufmerksamkeit einer großen Menge an Mathematikerinnen und Mathematikern zu erregen. Das gelang dagegen dem Künstler William Kolakoski. Der interessierte sich zwar sehr für Mathematik und Philosophie, studierte dann aber doch lieber Kunst. Trotzdem schickte er 1965 eine kurze Notiz an »The American Mathematical Monthly«. Darin wies er auf die Existenz der Zahlenreihe aus Einsen und Zweien hin – die er unabhängig von Oldenburger entdeckt hatte – und fragte nach einer einfachen Methode, um beschreiben zu können, wie man diese Folge berechnen könne und ob sie periodisch sei, sich also die Einträge irgendwann zu wiederholen beginnen.

Ob die Kolakoski-Sequenz, wie sie nun allgemein genannt wird, tatsächlich periodisch ist oder kein Muster zeigt, ist heute immer noch unbekannt. Ebenso unbekannt ist, ob im Grenzfall einer unendlichen langen Folge insgesamt mehr Einsen oder Zweien auftauchen oder beide gleich oft vorhanden sind.

Kolakoski selbst schätzte die Folge vor allem wegen ihrer ästhetischen und philosophischen Konsequenzen. Er litt sein Leben lang unter Schizophrenie und sah in der Sequenz eine seltsame Art der chaotischen Ordnung: Bei den Regeln, die sie erzeugen, gibt es keinen Interpretationsspielraum und dennoch verhält sich die Abfolge der Zahlen auf eine unvorhersehbare Weise.