Die Bekenstein-Hawking-Entropie bezeichnet einen Entropiebegriff, den man im Rahmen einer Thermodynamik bei Schwarzen Löchern definiert hat. Diese Ableitung gelang Stephen Hawking und wurde 1973 in der Publikation The Four Laws of Black Holes Mechanics veröffentlicht. Da er Bezug nahm auf Jacob D. Bekensteins Doktorarbeit (1972), wurde ihnen zu Ehren das Entropie-Analogon bei Schwarzen Löchern so genannt.

Fläche des Horizonts Schwarzer Löcher

In der Berechnung taucht eine Größe auf, die mit der kugelförmigen Oberfläche des Ereignishorizonts assoziiert werden kann:

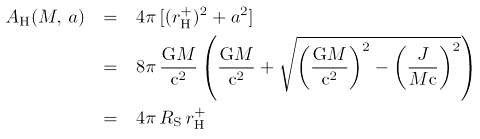
Dabei haben die Ereignishorizonte einen Radius, der gleich dem Schwarzschild-Radius R_S ist (nicht-rotierender Fall) oder der gleich dem äußeren Horizont r⁺_H ist (rotierender Fall):

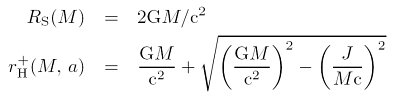
Die Oberfläche hängt im Allgemeinen sowohl von der Masse M als auch dem Drehimpuls J des Schwarzen Loches ab, so dass Schwarzschild-Lösung und Kerr-Lösung in dieser Hinsicht differieren müssen. Anschaulich ist das auch klar, denn der Radius des äußeren Horizonts r⁺_H wächst mit zunehmender Masse und abnehmendem Drehimpuls (Kerr-Löcher sind bei gleicher Masse kleiner als statische Schwarzschild-Löcher).

Entropiebegriff Schwarzer Löcher

Verschmelzen zwei Schwarze Löcher, so zeigt eine kurze Rechnung, dass die Oberfläche des neuen Horizontes größer ist, als die Summe der Flächeninhalte der einzelnen, kollidierenden Schwarzen Löcher. Das gilt auch bei den Entropien zweier verschmelzender Systeme. Die Entropie wird als proportional zu der Horizontoberfläche angenommen und führt zusammen mit dem Begriff der Hawking-Temperatur auf Analoga zu den vier Hauptsätzen der klassischen Thermodynamik. Für ein elektrisch neutrales, rotierendes Schwarzes Loch gilt:

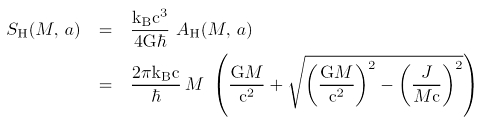
Die Gleichung oben zeigt gerade wie man die Bekenstein-Hawking-Entropie aus der Oberfläche des Horizonts A_H berechnet. Wie die Oberfläche von Masse und Drehimpuls abhängt, zeigt die erste Gleichung in diesem Eintrag. Setzt man ein statisches, d.h. nicht rotierendes Schwarzes Loch voraus (a = J/Mc = 0) folgt eine reine Massenabhängigkeit: eine quadratische Skalierung mit der Masse:

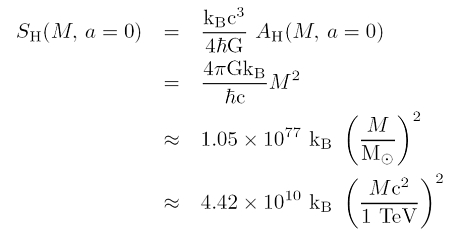
Entropien in Zahlenbeispielen

Einsetzen typischer Skalen der Astrophysik (eine Sonnenmasse) und Teilchenphysik (1 TeV) zeigt, dass die stellaren Schwarzen Löcher gigantische Entropien aufweisen, während Minilöcher, die in modernen Teilchenbeschleunigern entstehen könnten, moderate Bekenstein-Hawking Entropien haben. Bei supermassereichen Schwarzen Löcher erwartet man entsprechend noch höhere Entropien. Diese Zahlenwerte sind rätselhaft, denn die Größenordnung von 10⁷⁷ k_B für ein stellares Schwarzes Loch passt gar nicht zu der wesentlich kleineren Entropie des Vorläufersterns. Dieses Missverhältnis nennt man Entropie-Paradox Schwarzer Löcher oder auch Informationsverlustparadoxon.

Anlass für eine legendäre Wette

Dieses Paradoxon stand im Sommer 2004 im Fokus der Weltöffentlichkeit: Auf der Konferenz GR17 in Dublin, einer Zusammenkunft der führenden Relativisten und Gravitationsforscher der Welt, gab Hawking unter großem Medieninteresse bekannt, dass er sich geirrt habe und Schwarze Löcher nicht Information vernichten können. Damit gab er eine Wette verloren, die er mit seinen Wissenschaftskollegen Kip S. Thorne und John Preskill vor dreißig Jahren abgeschlossen hat. Vor allem Preskill, ein Quantentheoretiker, hielt an einer Erhaltung der Information fest – und bekam nun nach langer Zeit Recht. Thorne ist noch indefinit und möchte sich dem komplizierten Problem widmen. Auch unter Experten ist die Frage des Informationsverlusts umstritten und bedarf weiterer Analysen.

Entropien anderer Lösungen der Allgemeinen Relativitätstheorie

Gravasterne als reguläre Alternative ohne Horizont lösen dieses Paradox, weil sie kleinere Entropien haben. Denn die Gravastern-Entropie wächst nur linear mit der Masse. Allerdings müssten sich die Astrophysiker dann vom Konzept Schwarzes Loch verabschieden.

Literatur:

• Dissertation von J.D. Bekenstein, Princeton University (1972)
• Originalpapier von Bardeen, Carter & Hawking, The Four Laws of Black Holes Mechanics, Commun. Math. Phys. 31, 1973, 161 – 170
• Mazur & Mottola 2001, Papier Gravitational condensate stars: An alternative to black holes, gr-qc/0109035