Die Hawking-Temperatur ist ein Analogon zum thermodynamischen Temperaturbegriff, die man Schwarzen Löchern im Rahmen einer Thermodynamik (Wärmelehre) zuordnen kann. Diese Ableitung gelang Stephen Hawking und anderen Astrophysikern in den 70er Jahren des 20. Jahrhunderts (Publikation: The Four Laws of Black Holes Mechanics, 1973). Ebenso existieren für die Entropie Analoga bei Schwarzen Löchern. Bardeen, Carter und Hawking griffen dabei auf die Doktorarbeit von J.D. Bekenstein (1972) zurück und verallgemeinerten die darin enthaltenen Gleichungen. Seither nennt man das Entropie-Analogon bei Schwarzen Löchern Bekenstein-Hawking-Entropie. Es sei jedoch darauf hingewiesen, dass diese Analoga nicht zu verwechseln sind mit der gewöhnlichen, thermodynamischen Temperatur und gewöhnlichen, thermodynamischen Entropie eines Schwarzen Loches!

Bezug zu Eigenschaften Schwarzer Löcher

In den Rechnungen zeigte sich, dass die Hawking-Temperatur Schwarzer Löcher mit der Oberflächengravitation g_H und die Bekenstein-Hawking-Entropie mit der Oberfläche des Ereignishorizonts assoziiert ist. Der Drehimpuls (Rotation) eines Schwarzen Loches beeinflusst beide Größen, so dass für die Schwarzschild-Lösung andere Temperaturen/Entropien resultieren als für die Kerr-Lösung: Bei gleicher Masse unterscheiden sich demnach die Hawking-Temperaturen von statischen gegenüber rotierenden Löchern.

Oberflächengravitation

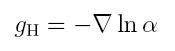Die Gleichung links entspricht der Definition der Oberflächengravitation als negativer Gradient des Logarithmus der Lapse-Funktion. Die Lapse-Funktion ist ein Maß dafür, wie für einen außenstehenden Beobachter der Zeitfluss verlangsamt wird. Ein bestimmter Beobachter, der so genannte FIDO, würde am Horizont eine verschwindende Lapse-Funktion und eine ins Unendliche gewachsene Oberflächengravitation sehen. Eine geeignete Renormierung der Zeitbasis führt auf die Oberflächengravitation, die Hawking und andere ableiteten.
Die Oberflächengravitation nimmt mit der Rotation eines Kerr-Loches ab, was man sich durch zunehmende Zentrifugalkräfte veranschaulichen kann, die die Oberflächengravitation absenken. Im Falle eines extremen Kerr-Loches mit maximaler Drehgeschwindigkeit (a = M in geometrisierten Einheiten, G = c = 1) ist sie sogar null: die ganze Masse bzw. Energie steckt dann in der Rotation. In diesem Sinne sind nicht rotierende Schwarze Löcher 'heißer'.

Nun zur Temperatur

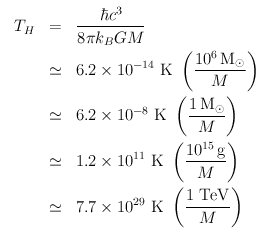Rechts steht die Gleichung, die für die Hawking-Temperatur abgeleitet wurde. Es ist ersichtlich, dass die Hawking-Temperatur nur von der Masse des Schwarzen Loches und einigen Naturkonstanten h (Plancksches Wirkungsquantum), c (Vakuumlichtgeschwindigkeit), k_B (Boltzmann-Konstante) und G (Gravitationskonstante) abhängt. Wesentlich ist, dass die Hawking-Temperatur linear mit abnehmender Masse des Lochs zunimmt:

Leichte Löcher sind heißer.

Das machen ein paar Zahlenbeispiele für Massen von Schwarzen Löchern klar, die gegenwärtig diskutiert werden und die unter der allgemeinen Gleichung rechts eingesetzt wurden: Sie zeigen, dass ein supermassereiches Schwarzes Loch von etwa einer Million Sonnenmassen (vergleichbar schwer wie das große Schwarze Loch im Zentrum der Milchstraße) eine verschwindend geringe Hawking-Temperatur hat, etwa ein Zehntel Billionstel Kelvin! Ein stellares Schwarzes Loch, das am Ende der Entwicklung massereicher Sterne steht, weist dagegen schon eine deutliche erhöhte Hawking-Temperatur auf, um hundert 'Nanokelvin'. Die primordialen Schwarzen Löcher, die möglicherweise im frühen Universum existierten, wiegen soviel wie ein irdischer Berg: eine Milliarde Tonnen. Für dieses Beispiel kann man sagen, dass sie tatsächlich mit etwa 100 Milliarden Kelvin Hawking-Temperatur heiß sind. Extrembeispiel sind die (hypothetischen!) Minilöcher, die auf den Skalen der Teilchenphysik liegen. Nimmt man an, dass sie so schwer sind wie etwa 1000 Protonen, resultiert eine enorme Hawking-Temperatur von etwa 10³⁰ Kelvin.

Wärmestrahlung

Ein Körper endlicher Temperatur emittiert immer Wärmestrahlung. Da der absolute Nullpunkt prinzipiell nicht erreichbar ist (3. Hauptsatz der Thermodynamik), gibt jedes Objekt Wärmestrahlung ab! Bei welcher Wellenlänge das Strahlungsmaximum liegt, bestimmt einzig und allein die Temperatur des Körpers (Wiensches Verschiebungsgesetz der Planckschen Strahlung). Extrem heiße Objekte, ab etwa eine Million Kelvin, können deshalb thermische Röntgenstrahlung abgeben; ein heißer O-Stern mit 30000 Kelvin Oberflächentemperatur (siehe dazu Spektraltyp) strahlt hingegen am meisten im UV ab.
Man kann die Hawking-Strahlung auch als Planck-Strahlung interpretieren, die ein Schwarzes Loch mit der Hawking-Temperatur aussendet. Die Zahlenbeispiele oben lassen sich dann so deuten, dass die Hawking-Strahlung von schweren Löchern kaum detektierbar sein wird, weil die Hawking-Temperatur so gering ist. Das Verschwinden von supermassereichen Schwarzen Löchern aufgrund des Verlusts durch Abstrahlung von Hawking-Emission ist ein sehr langwieriger Prozess und übersteigt das Alter des Universums bei weitem! Ganz anders stellt es sich bei den leichteren Löchern dar: Das Verdampfen durch Hawking-Strahlung, die Evaporation, geht hier deutlich schneller und sollte sogar nachweisbar sein. Denn das Ende des Verdampfungsprozesses ist so schnell, dass es einer Explosion gleichkommt. Die freigesetzte Leuchtkraft beträgt etwa 10²⁰ erg/s (Shapiro & Teukolsky 1983). Eine hohe Zahl solcher Explosionen im frühen Universum sollte deutliche Spuren in der Verteilung der kosmischen Hintergrundstrahlung hinterlassen haben – bislang wurde das jedoch nicht entdeckt.
Nullter und Dritter Hauptsatz der klassischen Thermodynamik können mit diesem Begriff der Hawking-Temperatur reformuliert werden und erhalten vollständige Analoga in der Theorie Schwarzer Löcher.

Weitere Literatur & Quellennachweise

• Web-Artikel: Schwarze Löcher – Das dunkelste Geheimnis der Gravitation, besonders das Kapitel Thermodynamik und Hawking-Strahlung
• Originalpapier von Bardeen, Carter & Hawking, The Four Laws of Black Holes Mechanics, Commun. Math. Phys. 31, 161, 1973
• M. Camenzind, LSW Heidelberg: Physik Rotierender Schwarzer Löcher, Vorlesungsskript Uni Heidelberg