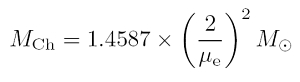Die Chandrasekhar-Grenze markiert die charakteristische Massengrenze für kompakte, stellare Objekte von etwa 1.4587 Sonnenmassen (mit einer geringfügigen Abhängigkeit von der chemischen Zusammensetzung). Die Bezeichnung wurde zu Ehren des indischen Astrophysikers Subrahmanyan Chandrasekhar (1910 – 1995) gewählt, der realistische Sternmodelle mit idealen Fermigasen bereits 1935 berechnet hat. Chandrasekhar gilt als einer der großen Relativisten und theoretischen Astrophysiker. 1983 erhielt er den Nobelpreis für Physik für seine Arbeit auf dem Gebiet des Sternaufbaus und der Sternentwicklung. Sein Buch The Mathematical Theory of Black Holes (1983) ist bis heute ein wichtiger Grundpfeiler der relativistischen Astrophysik und der Theorie der Schwarzen Löcher. Der amerikanische Röntgensatellit Chandra wurde ihm zu Ehren so getauft.

Ganz schön dicht

Diese Massendomäne kompakter Objekte ist gerade typisch für Weiße Zwerge, der kompakten Endkonfiguration eines massearmen Sterns, wie der Sonne. Das Elektronengas im Innern des Sterns wird erst bei hohen Dichten relativistisch, ab etwa 10⁶ g cm^-3. In normalen Sternen ist das nicht gegeben. Erst wenn er am Ende seiner stellaren Entwicklung im Gravitationskollaps kollabiert, kann der kompakte Kern im Innern ein relativistisches Elektronengas bilden. Die Objekte nahe an der Chandrasekhar-Grenzmasse sind daher typischerweise Weiße Zwerge. Aber auch viel leichteren Braunen Zwerge werden durch den Entartungsdruck stabilisiert.

Wenn Quanten drücken

Nein, hier drückt nicht der Schuh, sondern es sind quantenmechanische Teilchen, die sich gegen weitere Kompression wehren. Doch oberhalb der Chandrasekhar-Masse, kann der Stern nicht mehr durch den Entartungsdruck relativistischer Elektronen im hydrostatischen Gleichgewicht gehalten werden und muss zu einem noch kompakteren Objekt kollabieren, beispielsweise einem Neutronenstern, Magnetar, Quarkstern oder bei sehr großer Überschreitung der Massengrenze zu einem stellaren Schwarzen Loch (oder zu alternativen Objekten wie Gravasternen oder Holosternen?).

Quantenstatistik: Fermionen sind ungesellig

Es folgt nun eine kurze Skizzierung, wie man auf den Zahlenwert der Chandrasekhar-Grenze kommt. Erst die Fermi-Dirac-Statistik für Fermionen (Spin1/2-Teilchen), die 1926 entdeckt wurde, ermöglicht eine Beschreibung des Innern kompakter Objekte, die jedoch noch aus Elektronen, Nukleonen und Atomkernen bestehen. Anschaulich gesprochen kann man ein ideales Fermigas nicht beliebig komprimieren: das Pauli-Prinzip verbietet, dass Fermionen (wie Elekronen oder Neutronen) einen gleichen Quantenzustand besetzen können. Anders gesagt, setzen die Fermionen bei Kompression des Fermigases einen Druck entgegen, den Entartungsdruck der Elektronen. Der Entartungsdruck kann durch Integration über die Impulskugel von Impuls null bis zum Fermi-Impuls berechnet werden. Der Gravitationskollaps wird daher unterhalb der Chandrasekhar-Grenze gestoppt: es bildet sich eine stabile, stellare, aber kompakte Konfiguration aus: ein Weißer Zwerg.
Mathematisch geht man von der Bedingung für hydrostatisches Gleichgewicht aus und setzt eine polytropische Zustandsgleichung an. Die Einführung dimensionsloser Variablen führt dann auf die Lane-Emden-Gleichung, die fundamental ist in der Stellarphysik und numerisch gelöst werden kann. Die bekannten Gleichungen für Masse und Radius eines Sterns führen auf Masse-Radius-Beziehungen für entartete Sterne, die noch vom Polytropenindexn abhängen. Nun kann man zwei Regime unterscheiden:

• den nicht-relativistischen Fall n = 3/2
• und den relativistischen Fall n = 3.

Eine Frage der Zusammensetzung

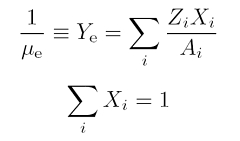Der letzte Fall für relativistische Elektronen, der typischerweise für Dichten größer als 10⁶ g cm^-3 erfüllt ist, zeigt keine Abhängigkeit mehr vom Radius bzw. von der Zentraldichte, sondern nur eine schwache Abhängigkeit von der chemischen Zusammensetzung (ausgedrückt durch den Parameter Y_e, siehe zweite Abbildung). Eine realistische Annahme aus der Kenntnis thermonuklearer Fusionsprozesse im Innern massearmer Sterne ist, dass infolge des Wasserstoffbrennens (siehe pp-Kette) und des CNO-Zyklus der kompakte Sternkern zu gleichen Teilen (Parameter X_i) aus Helium, Kohlenstoff und Sauerstoff besteht. Das führt gerade auf einen Parameter für die chemische Zusammensetzung von Y_e = 0.5 (wobei Z_i die Kernladungs- oder Ordnungszahl und A_i die Atommasse des Elements i bezeichnet). Bei diesem Zahlenwert kommt man auf die Chandrasekhar-Grenze, die dann bei 1.4587 Sonnenmassen liegt (siehe erste Abbildung). Diese Massengrenze kann durch starre Rotation des Weißen Zwergs nicht wesentlich verändert werden: die Zentrifugalkraft hat demnach keinen gravierenden Effekt in der Gleichung für hydrostatisches Gleichgewicht.
Die Weißen Zwerge befinden sich gerade am relativistischen Limit, so dass die eigentlich zu verwendenden Tolman-Oppenheimer-Volkoff-Gleichungen für das Innere des Weißen Zwergs nur eine kleine Korrektur bringen. Die Newtonsche Näherung reicht also aus.

Es geht noch dichter

Das Chandrasekhar-Modell erfährt eine Korrektur bei sehr hohen Zentraldichten ab 1.14 × 10⁹ g cm^-3. Dann setzt der inverse Beta-Zerfall ein. Dies wird ausführlich bei den Neutronensternen diskutiert, weil hier diese Reaktionen von höherer Relevanz sind.
Hamada und Salpeter haben 1961 Korrekturen zur Chandrasekhar-Theorie entarteter, relativistischer Sterne angebracht, die für ein Fermigas aus Elektronen und Atomkernen bis zu Dichten von etwa 10¹¹ g cm^-3 gelten. Die Elektronen sind dabei homogen in einem Ionengitter verteilt und wechselwirken miteinander über die klassische Coulomb-Wechselwirkung. Außerdem wechselwirken die Spins der Elektronen untereinander und können Energie austauschen. Daraus konnten sie die niedrigstmögliche Grenzmasse auf 1.015 Sonnenmassen bestimmen, ein Wert, der 1971 von Baym, Pethick und Sutherland im Wesentlichen bestätigt wurde.

Kohlenstoff-Sauerstoff- und Eisen-Zwerge

Die Hipparcos-Mission hat die Daten einiger Weißer Zwerge enthüllt, die sich in visuellen Binären befinden: die Masse folgt aus dem Dritten Kepler-Gesetz; der Radius kann aus dem gemessenen Fluss bei bekannter Distanz abgeleitet werden. Damit sind Masse-Radius-Beziehungen messbar! Legt man die obige Theorie zugrunde, zeigt sich, dass Weiße Zwerge im Wesentlichen entweder aus Kohlenstoff und Sauerstoff (CO-Zwerge, wie Sirius B und 40 Eri B) oder großteils aus einem Eisen-Kern bestehen (Fe-Zwerge, Procyon B, EG 50, GD 140). Letztgenannte sind wesentlich kompakter und haben kleinere Radien. Die Anreicherung mit Eisen stellt die Theorie der Sternentwicklung auf eine harte Probe, weil massearme Vorläufersterne (wie die Sonne), aus denen Weiße Zwerge hervorgehen, eigentlich gar kein Eisen in ihrem Innern fusionieren können!

Überschreiten der Chandrasekhar-Grenze?

2006 wurde ein Weißer Zwerg entdeckt, der vermutlich die Chandrasekhar-Grenze überschreitet. Das könnte funktionieren, falls der Zwerg außerordentlich schnell rotiert. Einzelheiten hierzu werden unter dem Eintrag Supernova, Abschnitt Zweifel an der Standardkerze SN Ia vorgestellt.