Der Holostern (engl. holostar) ist eine Lösung der Einsteinschen Feldgleichungen der Allgemeinen Relativitätstheorie (ART). Die Raumzeit der Holosterne wurde von dem Physiker Michael Petri 2003 vorgeschlagen. Alternative Bezeichnungen lauten holographisches Objekt, holographische Raumzeit oder holographische Lösung. Die holographische Lösung ist von Interesse in der relativistischen Astrophysik, weil diese Objekte astronomisch nach außen hin wie nicht rotierende Schwarze Löcher erscheinen, aber im Innern völlig andere Eigenschaften haben. Sie könnten sich auch relevant für die Kosmologie erweisen.

Eigenschaften

Die holographische Lösung ist eine statische und kugelsymmetrische Raumzeit. Die Raumzeit besteht aus drei unterschiedlichen Bereichen: die äußere Metrik entspricht der Schwarzschild-Lösung – das ist eine Folge des Birkhoff-Theorems. Im Gegensatz zum Schwarzen Loch haben Holosterne keinen Ereignishorizont. Der Krümmungsskalar (Ricci-Skala) divergiert bei Radius null. In diesem Sinne haben Holosterne eine Krümmungssingularität im Innern. Diese unterscheidet sich insofern von derjenigen Schwarzer Löcher, dass man die Singularität durch ein Quantenobjekt (z.B. einen String) ersetzen kann – bei Schwarzen Löchern funktioniert das nicht. Es gibt kein Entropie- bzw. Informationsparadox: Information geht nicht im Gravitationskollaps verloren, sondern bleibt bei der holographischen Lösung erhalten. Das sind entscheidende Unterschiede zum Schwarzen Loch! In den Augen einiger Astrophysiker sind das sehr attraktive Eigenschaften.
Holosterne weisen damit erstaunlich viele Ähnlichkeiten zu den Gravasternen (Mazur & Mottola 2001) auf. Es sei angemerkt, dass die Bezeichnung -stern in beiden Fällen, Holostern und Gravastern, etwas irreführend ist: Beide Objekte können – laut Theorie – ohne weiteres weit höhere Massen annehmen als Sterne. Damit kann nicht ausgeschlossen werden, dass sie – anstelle von supermassereichen Schwarzen Löchern – die Zentren von Galaxien bevölkern.

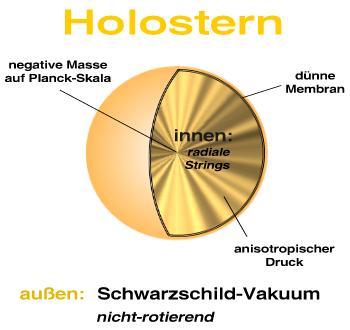
Anpirschen an den Holostern

Nähern wir uns nun von außen nach innen der Holostern-Metrik. Der Holostern wird im Außenbereich durch die klassische Schwarzschild-Metrik der ART beschrieben (siehe Illustration oben). Bei Erreichen eines Abstands, der vergleichbar mit dem Schwarzschild-Radius ist, gibt es etwas Neues: anstelle des Ereignishorizonts befindet sich hier, bei einem Radius r_h, eine Membran. Die Membran hat eine Dicke von null und kann als masselos betrachtet werden. Aber sie weist einen tangentialen (poloidalen) Druck auf. In der Membran herrscht eine Oberflächenspannung, weil sich der Druck in radialer Richtung abrupt ändert – das ist analog zur Oberflächenspannung eines Wassertropfens. Im Innern dieser Haut gibt es einen Bereich, in dem die Energiedichteverteilung einem 1/r²-Gesetz folgt. Solche Dichteverteilungen sind gerade das Wesen der holographischen Lösung. Petri zeigte 2006, dass ein reguläres, kugelsymmetrisches, holographisches Objekt eindeutig durch ein solches Gesamtenergiedichteprofil charakterisiert ist. Wie wir detaillierter besprechen werden, hat das Innere des holographischen Objekts Eigenschaften wie Stringmaterie.

Bezug zum holographischen Prinzip

Die Masse des Holosterns kann wie bei einem gewöhnlichen Stern durch die Summation über die Materiedichteverteilung berechnet werden. Alternativ kann die Masse ausschließlich durch die Betrachtung der Membran, also des Holosternrands, gefolgert werden. Die Äquivalenz beider Betrachtungsweisen ist gerade eine Konsequenz des holographischen Prinzips, dem der Holostern seinen Namen verdankt: Wie bei einem Hologramm können Eigenschaften eines Objekts höherer Raumdimension auf ein Abbild niedrigerer Raumdimension übertragen werden. Diese Projektion kennt man von der AdS/CFT-Korrespondenz in den Feldtheorien ('t Hooft & Susskind 1993/94; Maldacena 1997). Die AdS/CFT-Korrespondenz besagt, dass eine Quantengravitation auf dem Hintergrund einer Anti-de-Sitter (AdS) Raumzeit in fünf Dimensionen äquivalent ist zu einer konformen Feldtheorie (CFT) ohneGravitation auf dem Rand der AdS-Raumzeit, also in nur vier Dimensionen. Beim Holostern geschieht Ähnliches: Die Fläche seiner Membran ist entscheidend und bestimmt seine Masse. An dieser Stelle schließt sich der Kreis von holographischen Lösungen zur Thermodynamik Schwarzer Löcher, denn sie – insbesondere der Zusammenhang zwischen Fläche des Ereignishorizonts und Bekenstein-Hawking-Entropie – war gerade der Ausgangpunkt für 't Hooft's und Susskind's Überlegungen zum holographischen Prinzip.

Kein gleicher Druck in alle Richtungen

Der entscheidende Unterschied zum Gravastern ist nun eine anisotrope Druckverteilung im Innern des Holosterns, also innerhalb des Bereichs, der von der Membran umschlossen wird: Die radiale Druckkomponente entspricht gerade der negativen Dichte. Die senkrechte Druckkomponente ist eine Delta-Distribution, die am Membranradius einen Wert von 1/(16π r_h) annimmt. Im Innern verschwindet daher die (zum Radius) senkrechte Druckkomponente. Holosterne gehören also zur Klasse der anisotropen, kompakten Objekte. Die Anisotropie bezieht sich auf den Drucktensor, der als solcher der räumliche Anteil (Indizes i,k = 1,2,3) des Energie-Impuls-Tensors ist.
Der negative radiale Druck wurde anfangs so interpretiert, dass ein Teilchenstrom kontinuierlich radial in das Innere des Holosterns strömt. Petri favorisierte zunächst supersymmetrische (SUSY-) Teilchen, die einfallen und den negativen radialen Druck generieren – doch das ist nur ein möglicher Vorschlag, um die anisotrope Druckverteilung zu erklären. In diesem Szenario müsste es einen Mechanismus geben, der gewöhnliche, baryonische Materie in SUSY-Materie umwandelt. Womöglich spielt dabei die Membran die Schlüsselrolle.

Interpretation mit Strings

In einer weiteren Veröffentlichung griff Petri 2004 die Konzepte der Stringtheorien, insbesondere von Samir Mathur auf. Er erklärte den radialen Anteil des anisotropen Drucktensors im Innern des Holosterns dadurch, dass er möglicherweise mit radialen, fraktionierten Strings angefüllt sei. Fraktionierte Strings oder Branen sind String- bzw. Branenstücke, die Mathur eingeführt hat. Der Stringhypothese für Holosterne folgend, würden sich die Strings vom Zentrum bis nach außen zur Membran des Holosterns erstrecken. Die Zustandsgleichung dieser Stringmaterie hat gerade einen negativen radialen Druck. Wie aus der Kosmologie im Zusammenhang mit der Dunklen Energie bekannt, haben solche Zustandsgleichungen eine antigravitative Wirkung. Die Stringinterpretation ist jedoch nicht zwingend bei der holographischen Lösung; insofern wäre es falsch zu behaupten, dass Holosterne Stringmodelle sind – das innere Dichteprofil bietet allerdings eine interessante Assoziation mit Strings an.
Der Holostern hat rein formal eine Punktsingularität bei r = 0, weil dort der Ricci-Skalar unendlich wird. Dies ist sicherlich eine Eigenschaft von Holosternen, die diskutiert werden muss.

thermodynamische Aspekte

Die weitere Auswertung der Holostern-Lösung zeigte, dass deren Entropie bzw. Temperatur mindestens proportional, vielleicht sogar identisch mit Bekenstein-Hawking-Entropie bzw. Hawking-Temperatur sind (Petri 2003, 2004).
2006 betrachtete Petri die thermodynamische Stabilität der holographischen Lösung. Die freie Energie ist dabei die wesentliche Größe, weil ein thermodynamisch stabiles Objekt die freie Energie (und nicht nur die innere Energie) minimiert. Die freie Energiedichte ist im gesamten Holostern null, was als hohe thermodynamische Stabilität interpretiert werden kann. Allerdings ist thermodynamische Stabilität nicht gleich metrische Stabilität. Um diese Stabilität der Raumzeit zu zeigen, müssen Methoden der ART benutzt werden. Es wäre dann zu untersuchen, ob die holographische Metrik beispielsweise bei einer radialen Störung oszilliert und wieder in die statische Holosternmetrik zurück schwingt oder ob sie zur Schwarzschildmetrik kollabiert. Im letztgenannten Fall wäre der Holostern metrisch instabil.

Kosmologie mit holographischer Lösung

Petri schlägt sogar vor, die holographische Lösung anstelle der Friedmann-Weltmodelle in der Kosmologie als Modell für das ganze Universum zu verwenden. Das mag zunächst verwundern, weil man einen Widerspruch zwischen Ergebnissen der experimentellen Kosmologie mit expandierendem Kosmos und statischer Metrik der holographischen Raumzeit sehen könnte. Doch Petri zeigte, dass ein Beobachter auf einer Geodäte in einer ausreichend großen holographischen Metrik ein isotrop expandierendes Universum wahrnehmen würde. Der anisotrope Druck übernehme dabei die Rolle der kosmologischen Konstante als Antrieb der Expansion.
Interessanterweise reproduziert die holographische Raumzeit das beobachtete Verhältnis von Photonenzahl zu Elektronenzahl, nämlich eine Milliarde zu eins.
Wie weit holographische Universen tragen ist Gegenstand der Forschung.

Weitere Formen holographischer Raumzeiten

Es existiert in Analogie zur Reissner-Nordstrøm-Lösung auch der elektrisch geladene Holostern (Petri 2003). Die deutlich wichtigere rotierende Verallgemeinerung steht noch aus!

Welche Struktur hat das Vakuum?

Was Gravastern und Holostern so interessant für die Astrophysik macht, ist der Umstand, dass sie möglicherweise Alternativen zu den Schwarzen Löchern darstellen. Sie tragen der komplizierten Struktur des Vakuums Rechnung. Das relativistische Vakuum wird durch ein identisches Verschwinden des Energie-Impuls-Tensors realisiert. Die neueren Erkenntnisse über die Struktur des Vakuums im Rahmen der Quantentheorie (z.B. Casimir-Effekt) und der Stringtheorien legen nahe, dass für den Energie-Impuls-Tensor ein anderer Ansatz näher an der Natur ist, als der identisch verschwindende Energie-Impuls-Tensor in der klassischen Theorie. Während die Gravasterne Ausfluss der Quantengravitation von Mazur & Mottola sind, verfolgt Petri bei den Holosternen einen thermodynamischen Ansatz, der mit den Stringtheorien verträglich zu sein scheint.

Verhaltene Skepsis in der scientific community

Trotz dieser interessanten und diskussionswerten Eigenschaften der holographischen Raumzeiten, ist die Reaktion der meisten Wissenschaftler recht zurückhaltend. Das hat unterschiedliche Gründe: Generell gilt, dass sich neue Vorschläge schwer etablieren – es sei denn ihre Brauchbarkeit erweist sich unmittelbar, z.B. weil sie ein Experiment bestens erklären. Im Falle von Grava- und Holostern gibt es zwei Gründe für die Skepsis: Zum einen wurde noch nicht überzeugend dargelegt, dass diese Raumzeiten wirklich metrisch stabil sind. Es genügt nicht Lösung der Einsteinschen Feldgleichung zu sein, die Lösung darf 'nicht in sich zusammenfallen' und dann beispielsweise doch wieder der Schwarzschild-Metrik entsprechen. Zum anderen rotieren die Grava- und Holosterne nicht. Insofern repräsentieren sie nur eine echte Alternative zur Schwarzschild-Lösung. Sie können also bislang nicht die Eigenschaften rotierender Raumzeiten wie der Kerr-Lösung ersetzen. Die Astrophysik der Aktiven Galaktischen Kerne (AGN) zeigt jedoch, dass diese Rotationseigenschaft unabdinglich ist, um die Jetsmagnetohydrodynamisch zu erzeugen. Die Magnetosphärenphysik in der Ergosphäre (z.B. Blandford-Znajek-Mechanismus, Penrose-Prozesse) ist der Schlüssel, um magnetisch getriebene Jets zu erhalten. Die Bildung dieser Plasmaströme, wie man sie in Radiogalaxien, radiolauten Quasaren und Blazaren beobachtet, folgt aus dem AGN-Paradigma. Auch bei Mikroquasaren und Gammastrahlenausbrüchen wird die schnell rotierende Raumzeit zum Antrieb der stellaren Jets benötigt. Gelänge es Grava- und Holosterne rotieren zu lassen, würde das ihre Stellung in der Wissenschaft stärken.

Krise Schwarzer Löcher?

Wie die Gravasterne 2001, forcieren auch die Holosterne Widersprüche in der Physik Schwarzer Löcher. Eine besondere Problematik dabei ist, dass die astronomische Beobachtung es derzeit nicht gestattet, Kandidaten für statische Schwarze Löcher von Gravasternen oder Holosternen zu unterscheiden. Denn: die Gravitationsrotverschiebung verhindert eine gute Sicht für einen Außenbeobachter auf die Umgebung nahe dem Ereignishorizont! Die Hoffnung besteht darin, dass neue Unterscheidungskriterien bei der Erforschung der alternativen Raumzeiten offen gelegt werden. So sind Unterschiede in der Akkretion und bei der Emission von Gravitationswellen zu erwarten. Theoretische Studien haben gezeigt, dass die beobachteten Gravitationswellenformen es im Prinzip erlauben, den Ereignishorizont nachzuweisen (Berti & Cardoso 2006). Doch leider wurden Gravitationswellen bislang nicht direkt beobachtet, sondern nur indirekt – ohne Chance, auf die Wellencharakteristik schließen zu können.
In den Fällen, wo die Astronomen eine Rotation von Schwarzen Löchern nachgewiesen haben – und das sind bereits einige – können die Theoretiker derzeit nur die Kerr-Raumzeit zur Erklärung der Beobachtung heranziehen.

Papiere

• Petri, M.: The holostar – a self-consistent model for a compact self-gravitating object, 2003; Preprint unter gr-qc/0306066
• Petri, M.: Holostar thermodynamics, 2003; Preprint unter gr-qc/0306067
• Petri, M.: Charged holostars, 2003; Preprint unter gr-qc/0306068
• Mathur, S.D.: Where are the states of a black hole?, 2004; Preprint unter hep-th/0401115
• Petri, M.: The holographic solution – Why general relativity must be understood in terms of strings, 2004; Preprint unter gr-qc/0405007
• Petri, M.: On the thermodynamic origin of the Hawking entropy and a measurement of the Hawking temperature, 2004; Preprint unter gr-qc/0405008
• Petri, M.: Holographic spherically symmetric metrics, 2006; submitted to IJMPE