Massenwirkungsgesetz, Abk. MWG, Gesetz über die Gleichgewichtskonzentrationen einer chem. Reaktion, das lautet: Das Produkt aus den Konzentrationen der Endstoffe, dividiert durch das Produkt der Konzentrationen der Ausgangsstoffe im chem. Gleichgewicht ist eine Konstante, die Gleichgewichts- oder Massenwirkungskonstante K_c. Dabei treten die stöchiometrischen Koeffizienten als Exponenten der zugehörigen Konzentrationen auf. Das M. gilt in dieser Form nur für ideale Mischungen. Treten zwischen den Teilchen Wechselwirkungen auf, ist K_c nicht mehr konstant, sondern verändert sich mit den Anfangskonzentrationen. Deshalb werden anstelle der Konzentrationen die Aktivitätena_i eingeführt.

Für die allgemeine chem. Reaktion

lautet das M. in strenger Form

Dabei sind ν_i stöchiometrische Faktoren, die als Exponenten der zugehörigen Aktivitäten auftreten. Die ν_i der Ausgangsstoffe sind nach der thermodynamischen Vorzeichenkonvention negativ, gehen aber im M. positiv ein (|ν_A|,|ν_B|). Die Massenwirkungskonstante ist für jede chem. Reaktion eine charakteristische Konstante, die nicht von den Mengen und Mischungsverhältnissen der Reaktanten abhängt, sich aber mit der Temperatur und dem Druck ändert. Beteiligen sich bei heterogenen Reaktionen kondensierte Phasen reiner Stoffe am Gleichgewicht, ist zu beachten, daß die Aktivitäten reiner Stoffe definitionsgemäß gleich eins sind, d. h., sie treten im M. nicht auf. So gilt z. B. für das Boudouard-Gleichgewicht CO₂ + C

2 CO; K_a = a²_CO/a_CO2, da a_c = 1.

Wendet man das M. auf Reaktionen in idealen Mischungen an, so sind in den Aktivitäten a_i = f_ix_i die Aktivitätskoeffizienten f_i = 1, und das M. kann mit den Molenbrüchen x_i formuliert werden. Zur Kennzeichnung schreibt man für die Massenwirkungskonstante dann das Symbol K_x. Außerdem ist eine Umrechnung der Molenbrüche auf andere Zusammensetzungsgrößen möglich, z. B. auf Konzentrationen c_i, Molalitäten m_i, Partialdrücke p_i bei Gasreaktionen oder Stoffmengen n_i. Dabei ändern sich die Zahlenwerte und Einheiten der Massenwirkungskonstanten, die zur Unterscheidung mit dem jeweiligen Index (c, m, p, n) versehen werden. Es gelten folgende Zusammenhänge: a) für ideale Systeme K_a = K_x, b) für Gasreaktionen in idealen Mischungen K_x = K_pp_i-Σνⁱ = K_c(RT/p)Σνⁱ, c) für ideal verd. Lösungen K_x= K_c(M₁/ρ₁) _iΣνⁱ = K_m(M₁)Σνⁱ. Dabei sind Σν_i = ν_P + ν_Q – |ν_A| – |ν_B|, p der Gesamtdruck, R die Gaskonstante, T die absolute Temperatur, M₁ die Molmasse und ρ₁ die Dichte des Lösungsmittels. Für Reaktionen ohne Änderung der Molzahl, d. h. Σν_i = 0, sind alle K-Werte gleich und ohne Einheit.

Das M. läßt sich thermodynamisch aus der van't-Hoffschen Reaktionsisotherme Δ_RG = Δ_RG⁰ + RT Σν_iln a_i ableiten (Thermodynamik, 2. Hauptsatz, Anwendung d). Im Gleichgewicht ist die freie Reaktionsarbeit Δ_RG = 0, und es folgt K_a = e-ΔR^G0/RT, wobei Δ_RG⁰ die freie Reaktionsarbeit unter Standardbedingungen bezeichnet. Die letzte Beziehung bildet den Ausgangspunkt zur thermodynamischen Berechnung von Gleichgewichtskonstanten (Ulichsche Näherungen). Für die Temperaturabhängigkeit der Gleichgewichtskonstanten bei konstantem Druck folgt die van't-Hoffsche Reaktionsisobare.

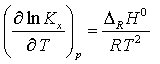
bei konstantem Volumen die van't-Hoffsche Reaktionsisochore

und für die Druckabhängigkeit von K_x bei konstanter Temperatur

mit Δ_RH⁰ = molare Reaktionsenthalpie, Δ_RU⁰ = molare Reaktionsenergie und Δ_RV⁰ = Änderung des Volumens der Mischung bei 1 mol Formelumsätzen (Le-Chateliersches Prinzip) jeweils unter Standardbedingungen.

Im Falle der formulierten Gleichgewichtsreaktion gilt für die Hinreaktion das kinetische Zeitgesetz r₁ = k₁c_A^|ν^A| c_B^|ν^B| und für die Rückreaktion r_-1 = k_-1c_Pν^Pc_Qν^Q, wobei r Reaktionsgeschwindigkeit und k Geschwindigkeitskonstante (Reaktionskinetik) bedeuten. Voraussetzung für die Formulierung der Zeitgesetze ist, daß beide Teilschritte Elementarreaktionen sind. Mit Hilfe des Prinzips der mikroskopischen Reversibilität (Gleichgewicht) läßt sich jedoch zeigen, daß diese Art der Ableitung auch auf komplexe Reaktionen übertragbar ist. Während der Einstellphase des Gleichgewichtes ist die effektiv meßbare Geschwindigkeit r = r₁ – r_-1. Im Gleichgewicht gilt r = 0. Hin- und Rückreaktionen verlaufen gleich schnell, makroskopisch findet keine Konzentrationsänderung mehr statt. Es liegt ein dynamisches Gleichgewicht vor. Es folgt

k₁c_A^|ν^A| c_B^|ν^B| = k_-1c_Pν^Pc_Qν^Q oder

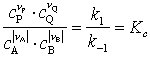
d. h. das M. mit der Gleichgewichtskonstanten K_c. Berücksichtigt man, daß für beide Geschwindigkeitskonstanten die Eyring-Gleichung gilt, so erhält man K_c = K₁/K_-1 = e^-(ΔG¹≠ – ΔG^-≠^1)/RT= e^-(ΔS¹≠ – ΔS-≠1)/R = e^-(ΔH¹≠ – ΔH-≠1)/RT wobei ΔG≠, ΔS≠ und ΔH≠ die freien Aktivierungsenthalpien, die Aktivierungsentropien und die Aktivierungsenthalpien von Hin- (1) und Rückreaktion (-1) bezeichnen. Durch Vergleich mit der Beziehung K_x= e-ΔR^G0/RT ergeben sich die folgenden Zusammenhänge zwischen den thermodynamischen Reaktionsgrößen und den kinetischen Aktivierungsparametern: Δ_RG⁰ = ΔG₁≠ – ΔG≠-1, Δ_RS⁰ = ΔS₁≠ – ΔS≠-1, und Δ_RH⁰ = ΔH₁≠ – ΔH≠-1.

Die Aussagen des M. können dazu dienen, die Ausbeute einer Reaktion gezielt zu beeinflussen, und zwar a) über die Konzentrationen (Aktivitäten) der Ausgangsstoffe bei unveränderten äußeren Bedingungen (K = konst.) und b) durch Veränderung von K aufgrund von Temperatur- und/oder Druckänderungen. a) Erhöht man die Konzentration eines Ausgangsstoffes, erfolgt so lange eine Reaktion in Richtung der Produkte, bis der Wert von K wieder erreicht ist, d. h., die Ausbeute steigt. Die wertvolleren Reaktanten können durch einen Überschuß der billigeren besser ausgenutzt werden. Den gleichen Effekt hat die ständige Entfernung von Produkten aus der Reaktionsmischung. b) Durch Veränderung von Temperatur oder Dr uck kann K vergrößert oder verkleinert und damit das Gleichgewicht in Richtung Produkte oder Ausgangsstoffe verschoben werden (Le-Chateliersches Prinzip).

Zur Anwendung des M. auf Elektrolytlösungen z. B. pH-Wert, Dissoziationskonstanten (Dissoziation) von Säuren und Basen, Ostwaldsches Verdünnungsgesetz, Löslichkeitsprodukt, Hydrolyse, Pufferlösung. Das M. bildet die Grundlage analytischer Meßmethoden und ermöglicht die Berechnung von Ausbeuten und deren gezielte Steuerung bei technischen Synthesen.