Multiplettstruktur, eine gegenüber dem Zentralfeldmodell verfeinerte Darstellung der energetischen Zustände in einem Mehrelektronenatom durch Berücksichtigung der elektrostatischen Elektronenwechselwirkung und der Spin-Bahn-Wechselwirkung. Im Zentralfeldmodell geht man von Einelektronenzuständen aus, die durch die Quantenzahlen n, l, m_l und m_s bestimmt sind. In dieser Näherung ergeben sich der gesamte Bahndrehimpuls L_L und der Gesamtspin L_s für ein Mehrelektronenatom als Summe der Bahndrehimpulse L_l bzw. der Spins L_s der einzelnen Elektronen. Man kann sich dabei auf die Valenzelektronen beschränken, da abgeschlossene Elektronenschalen keine Beiträge liefern. Die Quantenzahlen L und S bestimmen die Beträge der Vektoren L_L (gesamter Bahndrehimpuls) bzw. L_s (Gesamtspin). Für ein System mit zwei Elektronen gilt für die möglichen L,S-Werte L = |l₁ – l₂|, |l₁ – l₂| + 1, ..., l₁ + l₂ – 1, l₁ + l₂ bzw. S = |s₁ – s₂|, |s₁ – s₂| + 1, ..., s₁ + s₂ – 1, s₁ + s₂; wobei l₁, l₂ und s₁, s₂ die Quantenzahlen für die Beträge der Bahndrehimpulse L_l1, L_l2 und der Spins L_s1, L_s2 von beiden Elektronen sind. Die möglichen Orientierungen von L_L und L_s sind durch die Quantenzahlen M_L bzw. M_s bestimmt, die die Werte M_L = -L, -L + 1, ..., L – 1, L bzw. M_s = -S, -S + 1, ..., S – 1, S annehmen können. Die Betrags- und Orientierungsquantenzahlen L, S; M_L, M_s kennzeichnen Zustände Ψ_L,S,ML,MS der Elektronenhülle. Alle Zustände einer Elektronenkonfiguration mit gleichem L- und S-Wert nennt man Term. Für die Terme mit L = 0, 1, 2, 3, ... schreibt man die Buchstaben S, P, D, F, ... Zur Charakterisierung der Terme hinsichtlich ihres S-Wertes ist es üblich, die Multiplizität 2S + 1 links oben dem Termsymbol anzufügen. Terme mit den Multiplizitäten 2S + 1 = 1, 2, 3, ... bezeichnet man als Singulett (2S + 1 = 1), Dublett (2S + 1 = 2), Triplett (2S + 1 = 3) usw. Zu einem Term gehören (2L + 1) (2S + 1) Zustände. Betrachtet man zunächst ein System aus zwei nichtäquivalenten Elektronen (n₁ ≠ n₂), z. B. die Konfiguration 2p¹3p¹, so können L und S die Werte L = 0, 1, 2 bzw. S = 0, 1 annehmen. Es resultieren die Terme ¹S, ¹P, ¹D; ³S, ³P, ³D. Bei äquivalenten Elektronen (n₁ = n₂) ergeben sich durch die Ununterscheidbarkeit und das Pauli-Prinzip deutliche Einschränkungen der möglichen Terme (Tab.), da die Quantenzahlen m_l und m_s nicht frei kombinierbar sind. Ein Elektron bzw. ein fehlendes Elektron ("Loch") in einer Unterschale liefern den gleichen Beitrag zum Gesamtbahndrehimpuls und Gesamtspin.

Multiplettstruktur. Tab.: Mögliche Terme aus Konfigurationen mit äquivalenten Elektronen.

Durch die explizite Berücksichtigung der Elektronenwechselwirkung wird die Entartung der Terme einer Elektronenkonfiguration aufgehoben. Jeder Term ^2S+1L bleibt (2L + 1)(2S + 1)-fach entartet, da die Elektronenwechselwirkung die Kugelsymmetrie des Atoms nicht aufhebt und alle Zustände mit gleichem L und S, aber unterschiedlichem M_L und M_s die gleiche Energie haben. Genaue Aussagen über die energetische Lage der Terme sind nur anhand quantenmechanischer Rechnungen bzw. auf experimentellem Wege möglich. Aus empirischen Befunden wurde eine Regel zur Bestimmung des Terms mit der niedrigsten Energie, des Grundterms, aufgestellt. Danach hat der Term einer gegebenen Konfiguration mit dem größtmöglichen Wert von S und dem größten Wert von L, der mit dem maximalen S-Wert verträglich ist, die kleinste Energie (Hundsche Regel). Damit ergibt sich z. B. der ³P-Term als energetisch niedrigster Term der p²-Konfiguration (Abb.). Im Modell der unabhängigen Teilchen wird die Hundsche Regel vereinfacht häufig so wiedergegeben, daß im Grundzustand energetisch entartete Orbitale erst einfach durch Elektronen mit parallelem Spin (gleicher Spinquantenzahl m_s) besetzt werden. Neben der elektrostatischen Wechselwirkung zwischen den Elektronen treten in Atomen auch magnetische Wechselwirkungen (Spin-Bahn-Kopplung) auf. Diese äußern sich in kleinen Energieunterschieden zwischen Zuständen, deren Bahn- und Spindrehimpuls verschieden zueinander orientiert sind.

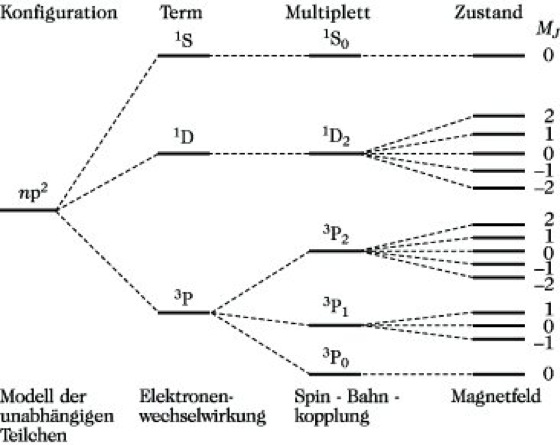
Multiplettstruktur. Abb.: Multiplettstruktur und Zeeman-Effekt für die np²-Konfiguration.

Alle Zustände, die sich bei gegebenen Werten von L und S nur durch die relative Orientierung von L_L und L_s zueinander unterscheiden, bilden ein Multiplett. Die durch die magnetische Wechselwirkung bedingte Aufspaltung der Terme bezeichnet man als Feinstruktur. Die Feinstrukturniveaus werden durch die Quantenzahlen J = L + S, L + S – 1, |L – S| bestimmt, die den Betrag des Gesamtdrehimpulses L_J festlegen. Sie werden als Index an das Termsymbol geschrieben: ^2S+1L_J. Für S ≤ L ergeben sich (2S + 1) und für S ≥ L (2L + 1) Feinstrukturniveaus. Die Richtungsquantelung des Gesamtdrehimpulses L_J wird durch die Quantenzahl M_J = -J, -J + 1, ..., J – 1, J bestimmt. Damit führt die Spin-Bahn-Kopplung zu einer Termaufspaltung in Komponenten ^2S+1L_J unterschiedlicher Energie, die jeweils (2J + 1)-fach entartet sind. So erhält man z. B. für den aus der p²-Konfiguration resultierenden ³P-Term (L = S = 1) die drei Komponenten ³P₂, ³P₁, ³P₀, da J die Werte 2, 1 und 0 annehmen kann. Das Kopplungsschema, bei dem zunächst die einzelnen Bahndrehimpulse L_l und Spins L_s der Elektronen zum gesamten Bahndrehimpuls L_L und Gesamtspin L_s der Elektronenhülle und dann erst diese zum Gesamtdrehimpuls L_J zusammengesetzt werden, heißt LS- oder Russell-Saunders-Kopplung. Sie ist für leichte und mittelschwere Atome eine gute Näherung. Bei schweren Atomen ist der entgegengesetzte Kopplungsgrenzfall (jj-Kopplung) von Bedeutung. Hier wird zunächst die Kopplung zwischen Bahn- und Spindrehimpuls jedes einzelnen Elektrons zum Gesamtdrehimpuls L_J betrachtet, und erst dann werden diese zum Gesamtdrehimpuls des Atoms L_J kombiniert. Bringt man ein Atom in ein äußeres homogenes Magnetfeld, so spaltet jedes Feinstrukturniveau ^2S+1L_J nochmals in 2J + 1 äquidistante Niveaus auf (Zeeman-Effekt). Dadurch wird die Entartung vollständig aufgehoben. Ausgehend von der p²-Konfiguration sind in der Abb. die verschiedenen Aufspaltungen dargestellt.