Wellenlängenmessung, Verfahren zur Bestimmung der Wellenlänge λ monochromatischen Lichtes (Laser). Je nach Art der Lichtquelle und gewünschter Genauigkeit werden verschiedene Methoden angewandt. Für den Genauigkeitsbereich δλ/λ≥10^-5 lassen sich Gitterspektrographen verwenden, wobei λ über genaue Winkelmessungen mit dem Goniometertisch erschlossen wird. Wenn α₀ den Winkel des einfallenden und α_m den Winkel des in m-ter Ordnung gebeugten Strahles mit der Normalen eines Plangitters bezeichnet, gilt λ=D(sinα₀+sinα_m)/m mit D als der Gitterkonstanten. Damit kann λ bei bekannten Werten von D und m aus den gemessenen Winkeln berechnet werden.

Höhere Meßgenauigkeiten lassen sich mit Interferometern erzielen. Insbesondere eignet sich das Fabry-Perot-Interferometer. Das Michelson-Interferometer läßt sich zur W. in ähnlicher Weise wie zur Längenmessung einsetzen (Interferenzlängenmessung). Große Verbreitung hat ein dynamischer Wellenlängenmesser gefunden. Dabei wird ein Schlitten, auf den zwei Tripelprismen montiert sind, mit konstanter Geschwindigkeit v längs einer vorgegebenen Strecke bewegt. Die Folge davon ist, daß sich die Interferenzstreifen über die jeweilige Detektoroberfläche verschieben (Abb. 1), wodurch Photoströme einen mit der Frequenz f_r=2v/λ_r bzw. f_u=2v/λ_u oszillierenden Anteil erhalten. Dabei bezeichnen λ_r die Wellenlänge eines Referenzlasers und λ_u die unbekannte Wellenlänge. Letztere ergibt sich aus der Beziehung λ_u=λ_rf_r/f_u. Die Meßgenauigkeit δλ/λ dieses Verfahrens liegt bei 5·10^-7. Sie kann durch elektronische Vervielfachung der Meßfrequenzen f_r und f_u bis auf etwa 10^-9 gesteigert werden. Man spricht dann von einem Lambdameter. Zu beachten ist, daß die obige Formel für λ_u nur für die Lichtausbreitung im Vakuum gilt. Bei Messungen in Luft müssen Brechzahlkorrekturen vorgenommen werden.

Dynamische Wellenlängenmesser sind in ihrer Anwendung auf kontinuierlich strahlende Lichtquellen beschränkt. Statische Wellenlängenmesser dagegen eignen sich für die Wellenlängenmessung an sowohl Impuls- als auch Dauerstrichlasern. Um eine hohe Meßgenauigkeit zu erreichen, benutzt man zur statischen Wellenlängenmessung mehrere Interferometer mit abgestufter Resonatorlänge. Geeignet sind Michelson-, Fizeau- und Fabry-Perot-Interferometer. In Abb. 2 ist eine Anordnung dargestellt, die sich aus drei Fabry-Perot-Etalons und einem Gitterpolychromator zusammensetzt. Das in den verschiedenen Ausgängen austretende Licht fällt auf Detektorzeilen (Photodiodenarrays) D₁, .., D₄, die aus jeweils 1024 Photodioden bestehen. Der Wellenlängenmessung liegt die Formel

zugrunde (Etalon), wobei λ₀ die Vakuumwellenlänge des Lichtes, d den Plattenabstand des Etalons, n den Brechungsindex des Plattenmaterials, m₁ die ganzzahlige Ordnungszahl für den innersten Haidingerschen Ring und e den Streifenüberschuß (Bruchteil der Ordnung) bezeichnen. Die Plattenabstände der drei Etalons, die von einem zum nächsten um einen Faktor 10 bis 20 anwachsen, werden durch Kalibrierung mit Licht unterschiedlicher, bekannter Wellenlängen bestimmt. Der jeweilige Streifenüberschuß e wird mit den Detektorzeilen D₁, D₂, D₃ gemessen. Er wird mit Hilfe eines Mikroprozessors aus dem gemessenen Radius von drei Ringen ermittelt. Ein gewisses Problem stellt die Bestimmung der Ordnungszahl m₁ dar. Dazu geht man wie folgt vor. Zunächst wird mit dem Polychromator ein erster Wert λ

für die Wellenlänge ermittelt. Dieser Näherungswert gestattet es, an Hand der obigen Formel die Ordnungszahl für das dünnste Etalon zu ermitteln. Diese Formel liefert dann durch Einsetzen des gemessenen Wertes für den Streifenüberschuß einen verbesserten Wert für die Wellenlänge, der es erlaubt, das Verfahren für das zweite Etalon und daran anschließend für das dritte (dickste) Etalon zu wiederholen. Statt mit Fabry-Perot-Etalons kann man in ähnlicher Weise auch mit Michelson- oder Vielstrahl-Fizeau-Interferometern arbeiten.

Eine Wellenlängenmessung mit einer relativen Genauigkeit δλ/λ≈10^-6 bis 10^-7 läßt sich bereits mit einem einzigen Zweistrahl-Fizeau-Interferometer ausführen (Abb. 3). An dem Keil, der von zwei in etwa 0,3 mm Abstand befindlichen, leicht gegeneinander geneigten Quarzglasscheiben gebildet wird, entstehen Interferenzstreifen gleicher Dicke, die mit einer CCD-Zeilenkamera registriert werden können. Mit Hilfe eines Mikrorechners wird die Lage der Interferenzmaxima ermittelt und daraus der Streifenabstand und die Phase des Interferenzmusters (das Argument des Kosinus, der die räumliche Modulation der Intensität beschreibt) an einem Referenzpunkte P bestimmt. Die gesuchte Wellenlänge λ₀ berechnet sich, wenn sich das Fizeau-Interferometer in einer Vakuumzelle befindet, nach der Formel 1/λ₀ = 2d(m+e), wobei d die dem Referenzpunkte P entsprechende Dicke des Keiles und m+e die in P vorliegende Ordnung der Interferenz bezeichnen. Der ganzzahlige Anteil m der Ordnung ergibt sich aus dem optischen Gangunterschiede in P und einem genäherten Wert für die Wellenlänge. Letzterer kann bei bekanntem Keilwinkel aus dem Streifenabstand berechnet oder durch dessen Vergleich mit dem bei einer Referenzwellenlänge gemessenen Streifenabstande bestimmt werden. Der Bruchteil e der Ordnung folgt aus der oben genannten Phase.

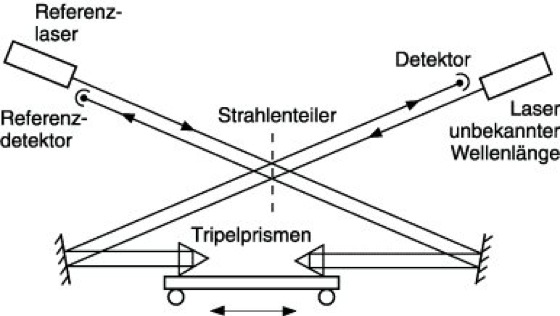
Wellenlängenmessung 1: Dynamisches Lambdameter nach dem Prinzip des Michelson-Interferometers.

Wellenlängenmessung 2: Mit drei Fabry-Perot-Etalons ausgestattetes Lambdameter. D₁, .., D₄ Detektorzeilen.

Wellenlängenmessung 3: Fizeau-Lambdameter.