Hemmes mathematische Rätsel: Welche Zahlen sind gesucht?

Bei einem alten Taschenrechner, der eine achtstellige Anzeige hat und bei dem die Zahlen durch 7-Segment-Ziffern dargestellt werden, sind alle vertikalen Segmente defekt. In diesen Taschenrechner wird eine Zahl eingetippt, und das Display zeigt die horizontalen Segmente aus dem oberen Bild. Nun wird die Maltaste gedrückt und anschließend eine zweite Zahl eingetippt. Das Display zeigt nun die horizontalen Segmente aus dem mittleren Bild. Nach dem Drücken der Gleichtaste zeigt das Display schließlich die horizontalen Segmente aus dem unteren Bild. Welche beiden Zahlen sind mit dem Taschenrechner multipliziert worden?
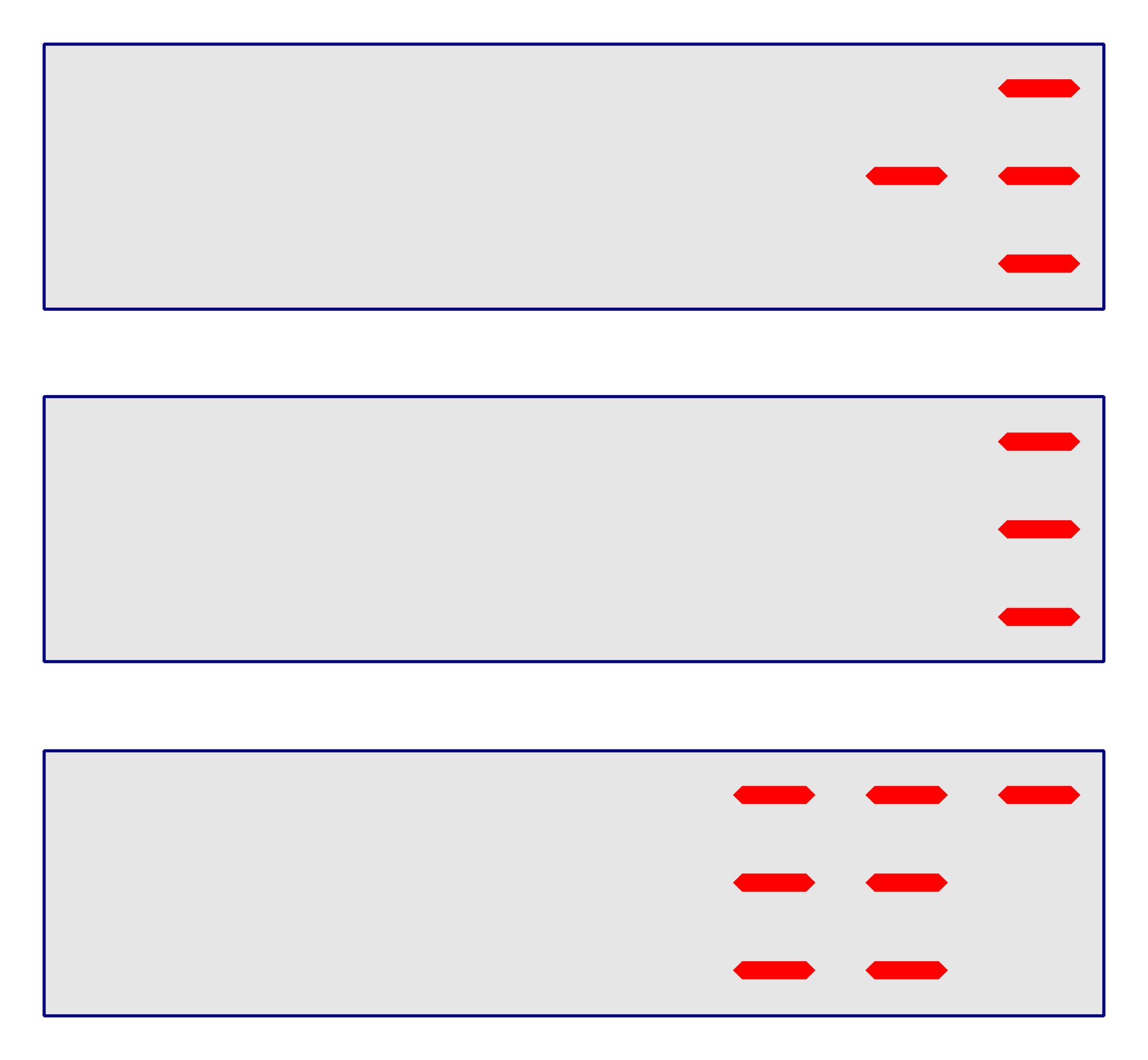
Die Endziffer des Produkts kann nur 7 sein. Da die Endziffern der beiden Faktoren nur 2, 3, 5, 6, 8 oder 9 sein können, muss ein Faktor auf 3 und der andere auf 9 enden. Die Zehnerziffer des ersten Faktors kann nur 4 sein. Somit könnte das Produkt 49 × 3 = 147 oder 43 × 9 = 387 sein. Die erste Möglichkeit scheidet jedoch aus, da die Hunderter- und Zehnerziffer des Produkts nur 2, 3, 5, 6, 8 oder 9 sein können. Alle drei Zahlen können jedoch noch führende Einsen besitzen, die unsichtbar wären. Mit höchstens einer führenden 1 pro Zahl findet man noch drei weitere Lösungen: 143 × 9 = 1287, 49 × 13 = 637 und 149 × 13 = 1937. Man kann leicht überprüfen, dass bei allen Faktoren mit mehr als einer führenden 1 das Produkt, abgesehen von den drei Endziffern, nicht aus lauter Einsen besteht.








Schreiben Sie uns!
Beitrag schreiben