Hemmes mathematische Rätsel: Welchen Flächeninhalt hat das blaue Quadrat?
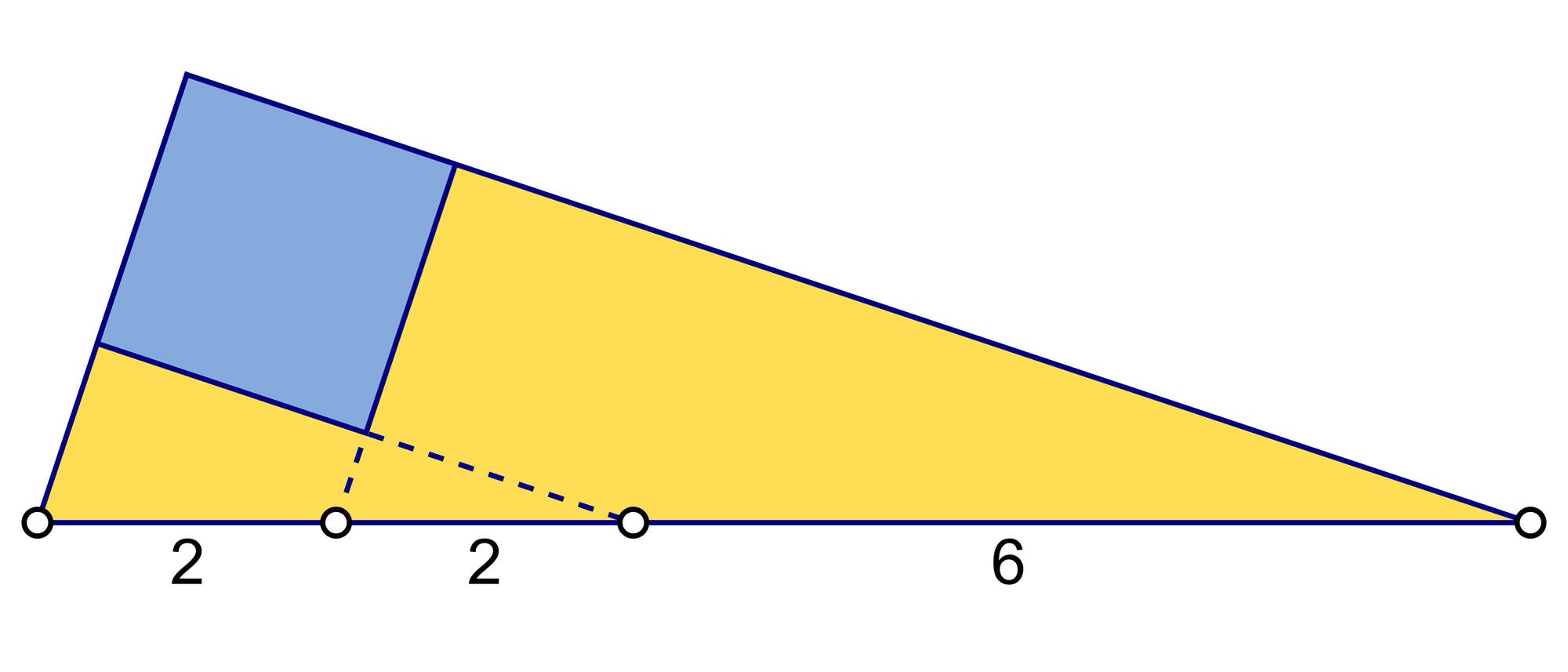
Das blaue Quadrat liegt in der rechtwinkligen Ecke eines rechtwinkligen Dreiecks. Die Verlängerungen seiner Seiten teilen die Hypotenuse des Dreiecks in drei Abschnitte der Längen 2, 2 und 6. Wie groß ist der Flächeninhalt des Quadrats?
Da die Strecken AB und CD parallel liegen und BD und DF gleich lang sind, müssen nach dem Strahlensatz auch AC und CF gleich lang sein. Folglich kann man neben das blaue Quadrat mit der Seitenlänge x noch ein zweites gleich großes Quadrat in das Dreieck einfügen. Die beiden rechtwinkligen Dreiecke CDF und EFG sind ähnlich. Somit gilt für das Verhältnis der langen Kathete zur Hypotenuse x/2 = y/6, woraus man y = 3x erhält. Für das Dreieck EFG erhält man mit dem Satz des Pythagoras x2 + y2 = 62. Setzt man das zuvor gefundene Ergebnis in diese Gleichung ein, bekommt man x2 + (3x)2 = 62, was man zu x2 = 18/5 zusammenfassen kann. Das blaue Quadrat hat somit einen Flächeninhalt von 18/5 = 3,6.
Schreiben Sie uns!
Beitrag schreiben