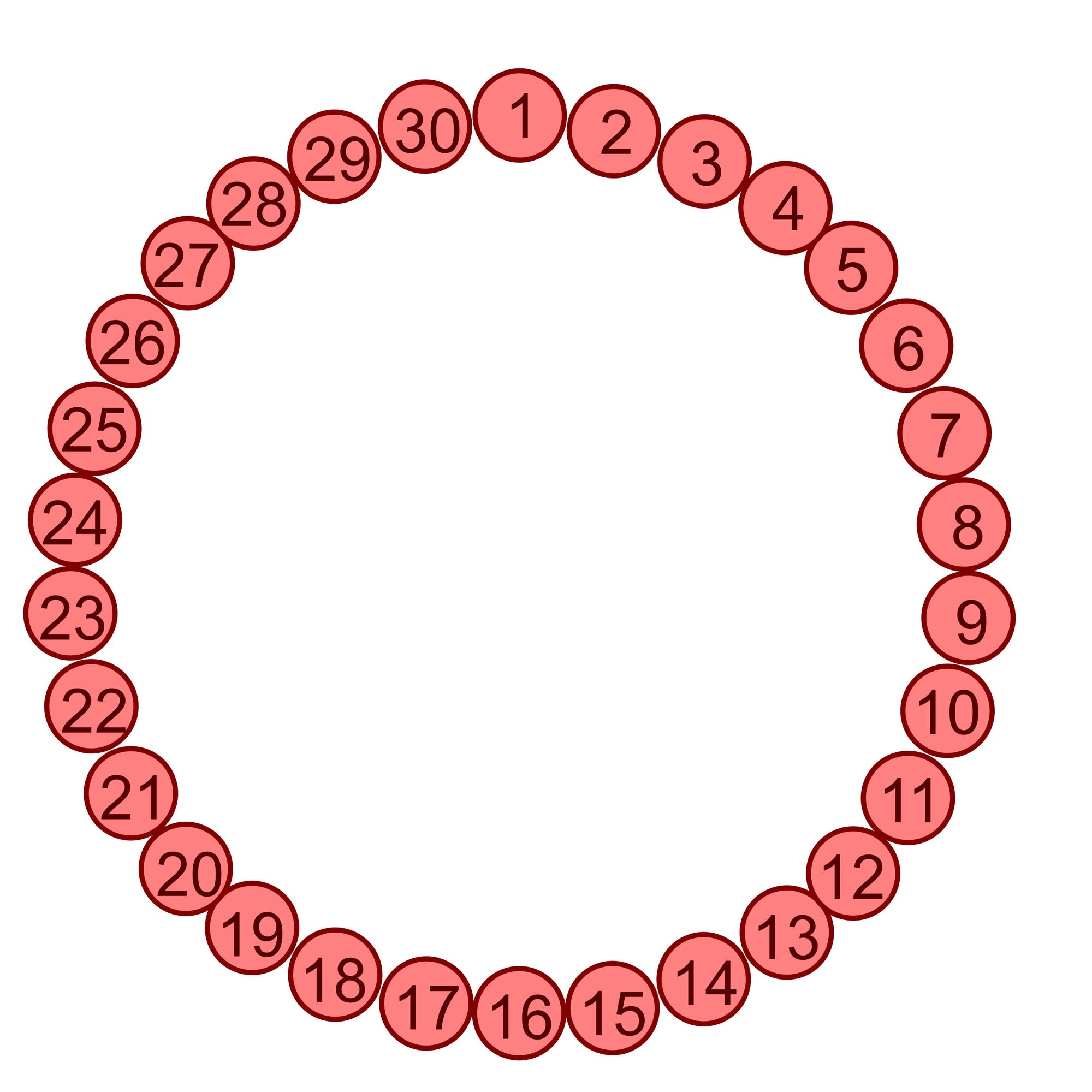
Wir können mit Sicherheit elf echte Münzen finden. Dazu beginnen wir an einer beliebigen Stelle und nummerieren die Münzen im Uhrzeigersinn durch. Von der Münze 1 bis zur Münze 11 liegen, einschließlich dieser beiden Münzen, im Uhrzeigersinn 11 Münzen und gegen den Uhrzeigersinn 21 Münzen. Dann legen wir die Münze 1 auf die linke Schale der Waage und die Münze 11 auf die rechte Schale. Bleiben die Schalen im Gleichgewicht, müssen beide Münzen echt sein, da es nur zehn falsche Münzen gibt. Da es andererseits nur 20 echte Münzen gibt, können nicht alle Münzen von Münze 11 bis Münze 1 im Uhrzeigersinn echt sein. Also sind alle elf Münzen von Münze 1 bis Münze 11 echt. Senkt sich hingegen die linke Schale, ist die Münze 1 echt und die Münze 11 falsch. Die falschen Münzen künnen nur im Bereich von Münze 2 bis Münze 20 liegen. Folglich sind die elf Münzen von Münze 21 bis Münze 1 echt. Senkt sich jedoch die rechte Schale, ist die Münze 11 echt und die Münze 1 falsch. Die falschen Münzen können nur im Bereich von Münze 22 bis Münze 10 liegen. Folglich sind die elf Münzen von Münze 11 bis Münze 21 echt.