Hemmes mathematische Rätsel: Welchen Flächeninhalt hat das Drachenviereck?
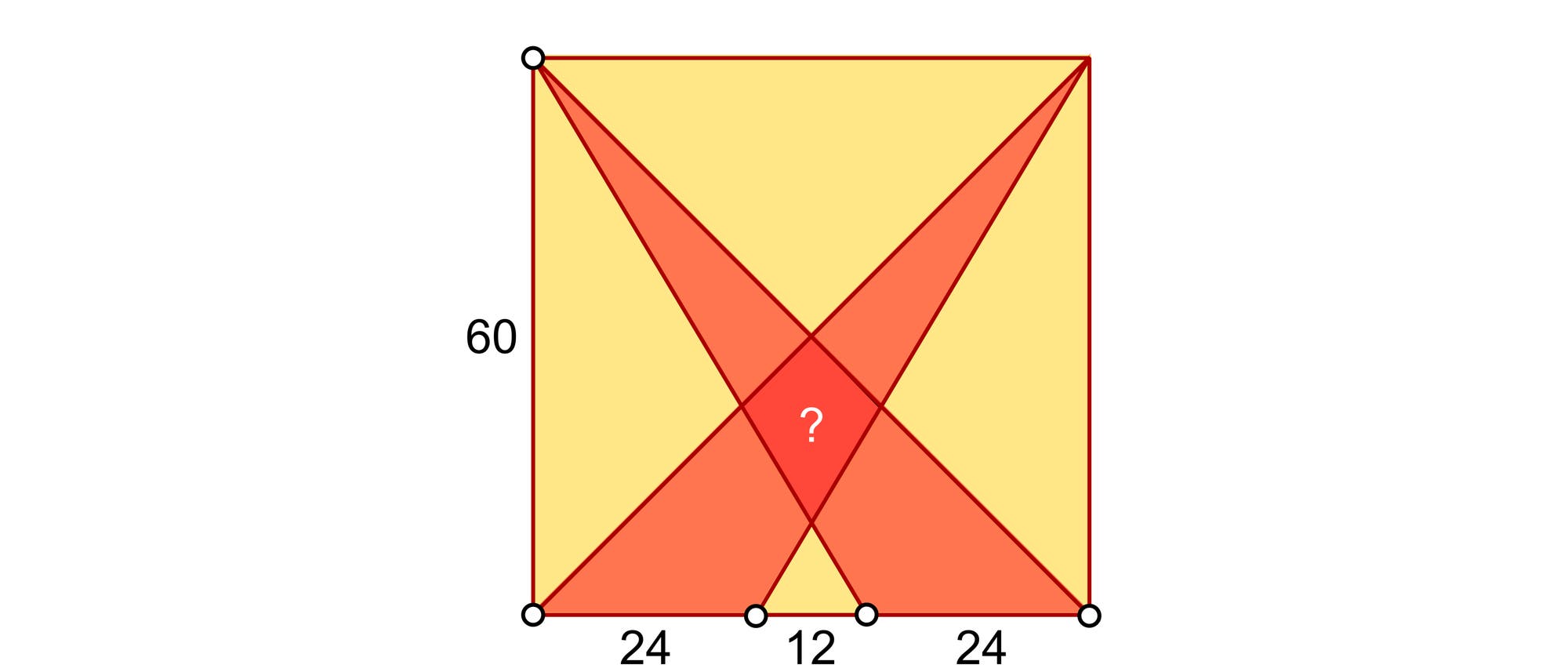
Die folgende Aufgabe stammt von Bernd Bultmann aus Butjadingen. Welchen Flächeninhalt hat das im Inneren des Quadrats liegende rote Drachenviereck?
H ist der Schnittpunkt der beiden Diagonalen des Quadrats, und somit ist HB = 30. Nach dem Strahlensatz gilt CB/AB = GF/AF oder CB = GF · AB / AF = 60 · 6 / 36 = 10. Damit hat die lange Diagonale des Drachenvierecks die Länge HC = HB – CB = 30 – 10 = 20. Das Dreieck EDF ist rechtwinklig und gleichschenklig. Folglich ist ED = DF = x. Nach dem Strahlensatz gilt ED/AD = GF/AF oder x/(AF – x) = GF/AF oder x/(36 – x) = 60/36. Dies kann man zu x = 45/2 auflösen. Damit beträgt die kurze Diagonale des Drachenvierecks IE = 60 – 2x = 15. Das Drachenviereck hat somit einen Flächeninhalt von 1/2 · IE · HC = 1/2 · 15 · 20 = 150.
Hat Ihnen dieses Rätsel gefallen? Dann rätseln Sie doch einfach direkt weiter:
- Welche sechsstelligen Zahlen sind gesucht?
- Wie groß ist die Fläche des Trapezes?
- Wie können die Zahlen noch verteilt werden?
- Warum stimmt diese Aussage?
- Wie lang ist die Sehne des Kreises?
- Welche Zahl fehlt?
- Wie kann das Rätsel gelöst werden?
- Wie viele dieser Zahlen gibt es?
- Wie viel deckt das Quadrat ab?
- Wie muss das Streichholz umgelegt werden?
- Welche Uhrzeit ist gesucht?
- Wie viel Prozent decken die Preise ab?
Eine Übersicht über alle Matherätsel finden Sie unter https://www.spektrum.de/raetsel/. Viel Spaß beim Weiterknobeln!
Schreiben Sie uns!
Beitrag schreiben