Hemmes mathematische Rätsel: Wie groß ist der Flächeninhalt des großen gelben Rechtecks?
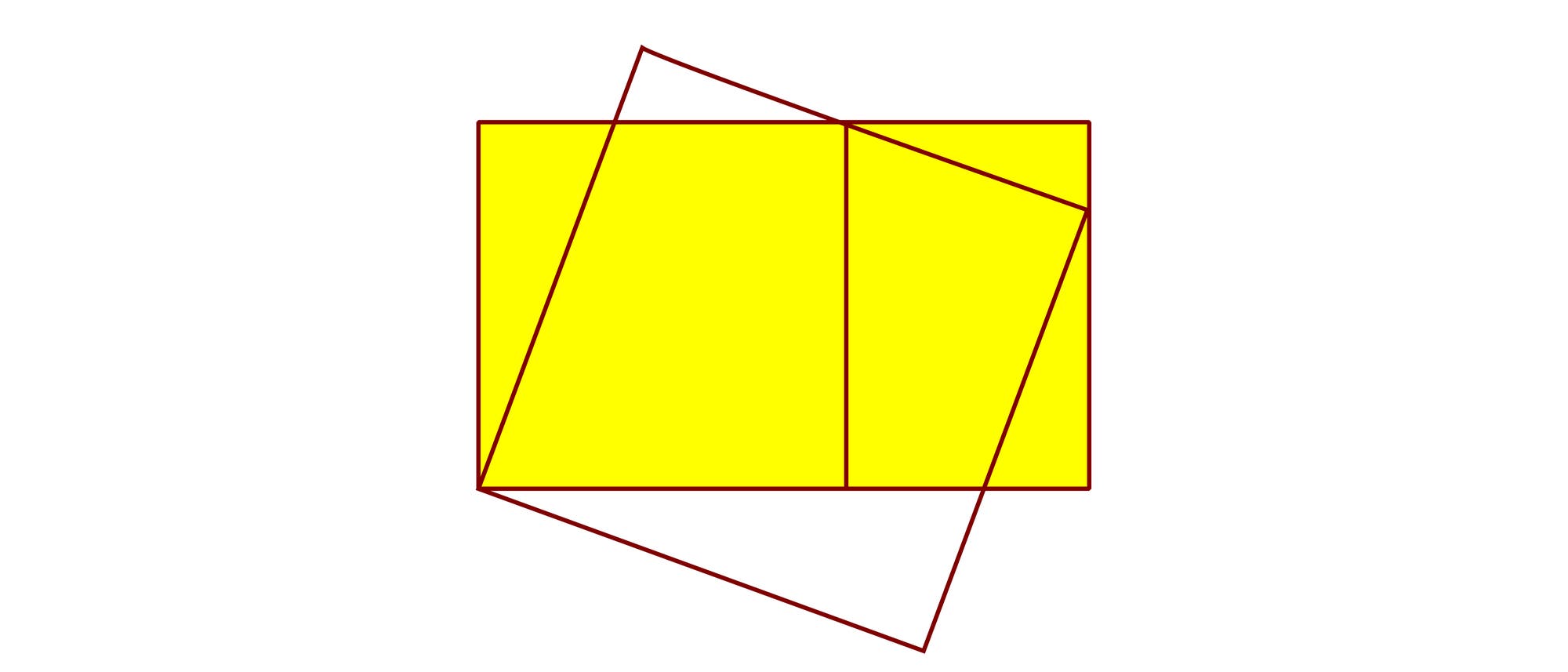
Das gelbe Rechteck aus dem Bild setzt sich aus einem kleinen gelben Quadrat und einem kleinen gelben Rechteck zusammen. Ein großes Quadrat mit der Seitenlänge 1 liegt so auf dem großen Rechteck, dass seine linke Ecke auf die linke untere Ecke des Rechtecks fällt und seine rechte Ecke auf die rechte Seite des Rechtecks. Die beiden anderen Ecken des großen Quadrats liegen oberhalb und unterhalb des Rechtecks. Die obere rechte Seite des großen Quadrats läuft durch die obere rechte Ecke des kleinen gelben Quadrats. Wie groß ist der Flächeninhalt des großen Rechtecks?
Hat das gelbe Quadrat ABCG die Seitenlänge y und das kleine gelbe Rechteck GCDF die Seitenlängen x und y, so hat das große gelbe Rechteck ABDF den Flächeninhalt (x + y)y. Durch die zusätzlichen Linien BG und BE entstehen die beiden rechtwinkligen Dreiecke BGH und EBI. Die beiden blauen Winkel sind gleich groß und auch die beiden Winkel EBH und IBE sind mit 45° gleich groß. Folglich müssen auch die beiden Winkel GBH und DBE gleich groß sein. Somit sind die Dreiecke BGH und BDE ähnlich. Die Hypotenuse BG des Dreiecks BGH hat die Länge y√2 und die Hypotenuse BE des Dreiecks BDE die Länge √2. Da die beiden Dreiecke ähnlich sind, sind die Verhältnisse ihrer jeweils langen Kathete zu ihrer Hypotenuse gleich. Es gilt somit BH/BG = BD/BE oder 1/(y√2) = (x + y)/√2, was sich zu (x + y)y = 1 umformen lässt. Das Quadrat und das Rechteck haben folglich gleich große Flächeninhalte.
Schreiben Sie uns!
Beitrag schreiben