Hemmes mathematische Rätsel: Wie groß ist die vierte Fläche?
2020 dachte sich Manfred Pietsch aus Kreuzau in Nordrhein-Westfalen ein geometrisches Problem aus, das im selben Jahr in der »Aachener Zeitung« und in den »Aachener Nachrichten« erstmals veröffentlicht wurde.
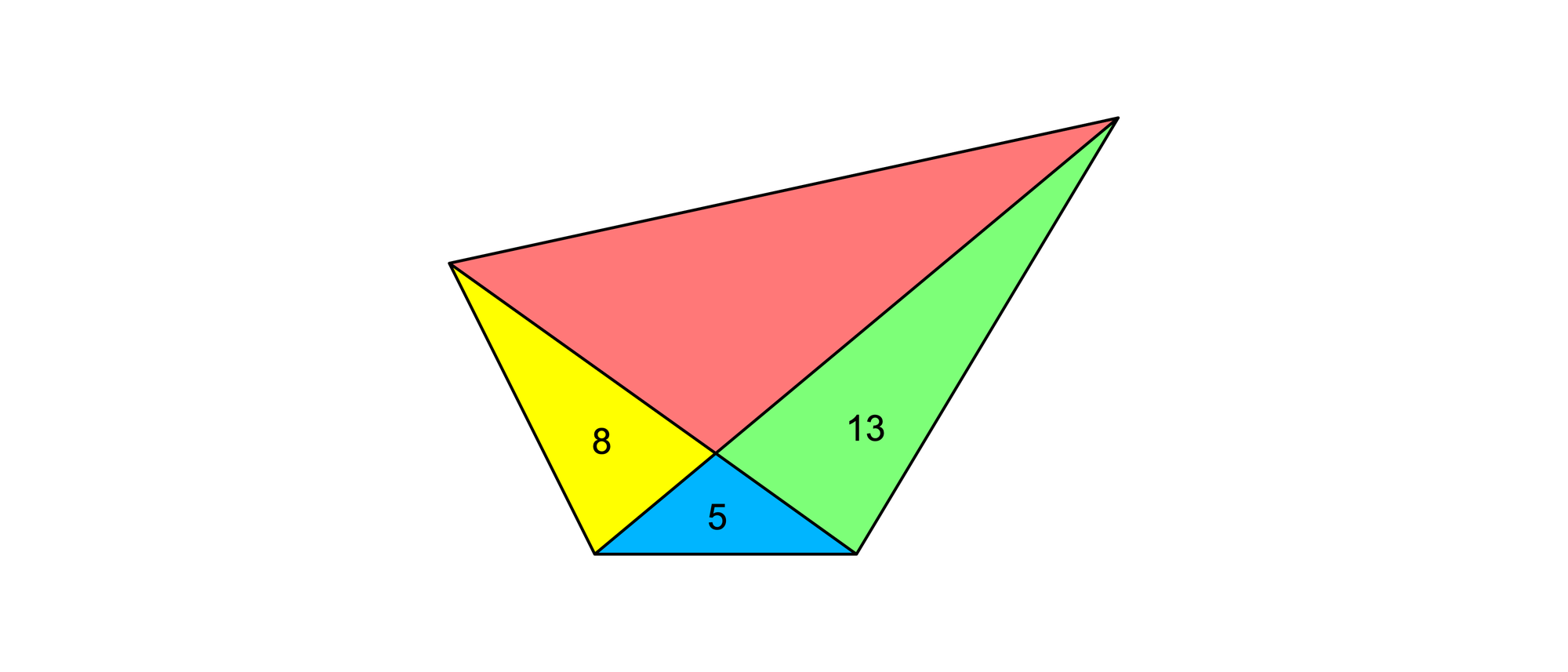
Ein Viereck wird durch seine beiden Diagonalen in vier Teilflächen zerlegt. Drei der Flächen haben die Inhalte 5, 8 und 13. Wie groß ist die vierte Fläche?
Betrachtet man die Strecken AS und SC als Grundseiten der vier Dreiecke, so gilt für die Flächeninhalte des grünen und des blauen Dreiecks SC · h/2 = 13 und AS · h/2 = 5, wobei h die gemeinsame Höhe ist. Daraus ergibt sich 13/5 = SC / AS.
Für das rote und das gelbe Dreieck mit der gemeinsamen Höhe k gilt entsprechend F/8 = SC / AS und damit auch F/8 = 13/5. Daraus ergibt sich der Flächeninhalt des roten Dreiecks zu F = 20,8.
Schreiben Sie uns!
Beitrag schreiben