Hemmes mathematische Rätsel: Wie viele Würfel erhält man?
Spielwürfel, wie wir sie beim Mensch-ärgere-dich-nicht-Spiel benutzen, kennt man seit Jahrtausenden. Die ältesten sechsseitigen Würfel, die Archäologen ausgegraben haben, stammen aus dem 3. Jahrtausend v. Chr. aus Tepe Gawra im Irak und aus Mohenjo-Daro in Pakistan. Sie haben bereits die Form eines Kubus und sind mit Augen gekennzeichnet. Bei den meisten antiken und bei allen modernen Würfeln sind die Zahlen von 1 bis 6 so verteilt, dass die Summe der Zahlen auf sich gegenüberliegenden Flächen jeweils 7 ergibt. Unter diesen Bedingungen gibt es zwei verschiedene Verteilungen der Zahlen auf den Flächen.
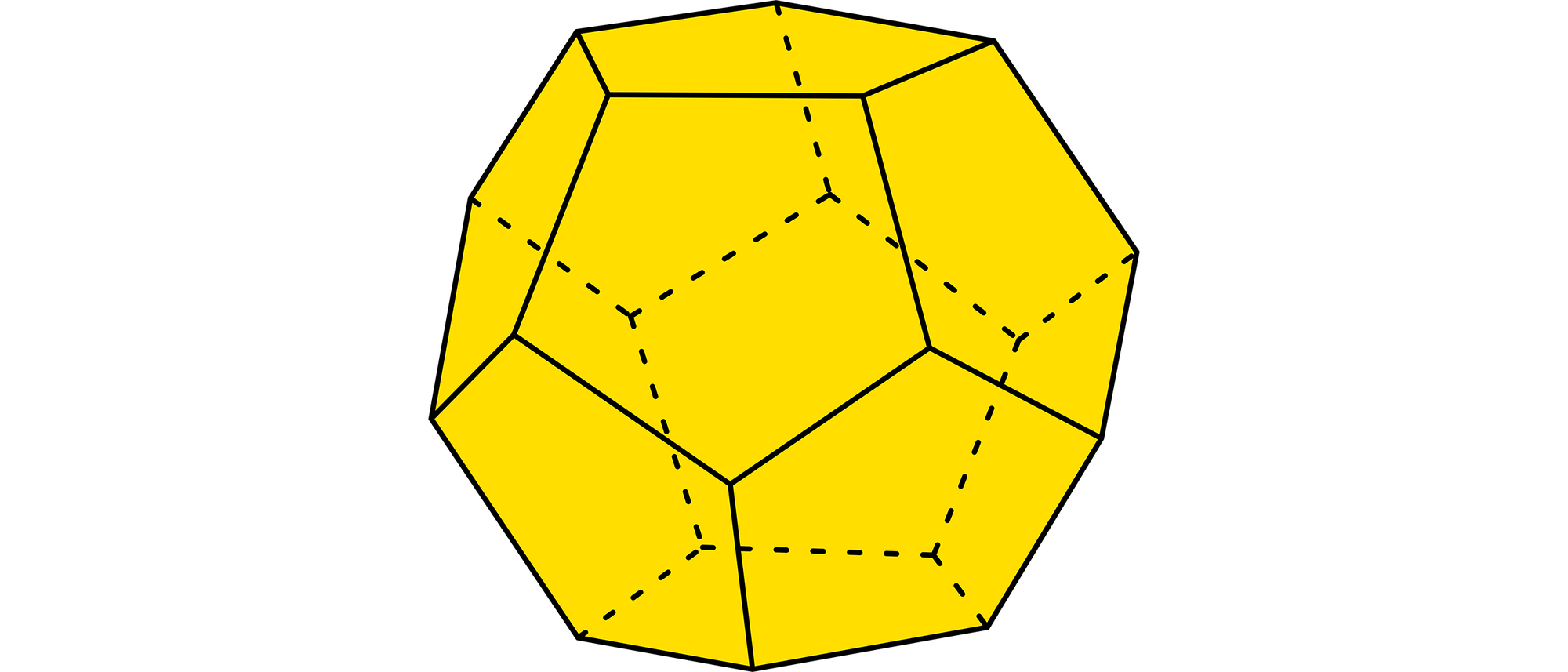
Hält man einen Würfel so, dass man genau auf die Ecke schaut, an der die Flächen mit den Zahlen 1, 2 und 3 zusammenstoßen, können die Zahlen 1, 2 und 3 im oder gegen den Uhrzeigersinn diese Ecke umlaufen. Spielwürfel müssen keine Hexaeder sein. Auch reguläre Dodekaeder, die zwölf gleichseitige Fünfecke als Flächen haben, können Spielwürfel sein. Ihre Seitenflächen tragen dann die Zahlen von 1 bis 12, und die Zahlen auf sich gegenüberliegenden Seiten ergänzen sich stets zu 13. Wie viele verschiedene solcher dodekaedrischen Würfel sind unter diesen Bedingungen möglich?
Wir bauen die Lösung systematisch auf und legen einen unbeschrifteten dodekaedrischen Würfel auf den Tisch. Auf die oberste Fläche schreiben wir nun die 1. Nun müssen wir die 12 auf die unterste Fläche schreiben, damit die Summe der Zahlen auf den beiden sich gegenüberliegenden Flächen 13 ergibt. Für die 2 stehen jetzt noch 10 Flächen zur Auswahl. Haben wir uns für eine Fläche entschieden, müssen wir die 11 auf die gegenüberliegende Fläche schreiben. Jetzt stehen für die 3 nur noch 8 Flächen zur Auswahl. Nach diesem Muster geht es weiter: Wir haben für die 4, 5 und 6 eine immer kleiner werdende Auswahl von Flächen. Die Flächen für die Ergänzungen 9, 8 und 7 zu 13 stehen damit jedes Mal fest. Somit gibt es N = 10 · 8 · 6 · 4 · 2 Möglichkeiten, das Dodekaeder zu beschriften. Wir haben jedoch jede Möglichkeit fünffach gezählt, denn wenn man das Dodekaeder um 360°/5 = 72° oder 2 · 72° oder 3 · 72° oder 4 · 2° um seine senkrechte Achse dreht, geht es in sich selbst über. Somit gibt es tatsächlich nur N/5 = 768 verschiedene dodekaedrische Würfel.
Schreiben Sie uns!
Beitrag schreiben