LFE-Beziehungen, Abk. für lineare Beziehungen der Freien Enthalpie (oder Freien Energie), eine Gruppe von empirischen Gleichungen, die Beziehungen zwischen der Struktur von Molekülen und bestimmten thermodynamischen oder kinetischen Eigenschaften (i. allg. der Reaktivität) herstellt. Die Korrelationen gelten in der Regel nur innerhalb einer Reihe ähnlicher Reaktionen. L. existieren für Gleichgewichts- und Geschwindigkeitskonstanten, aber auch für polarographische Halbstufenpotentiale, Infrarotfrequenzen, chem. Verschiebungen in der Kernresonanzspektroskopie oder Lösungsmitteleinflüsse auf Reaktionsgeschwindigkeiten.

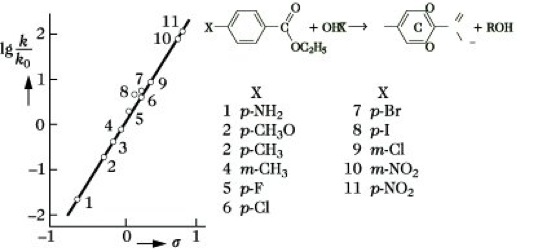
LFE-Beziehungen. Abb.: Hammett-Korrelation für die Reaktionen.

L. haben meist die Form lg k₁ = a lg k₂ + b. Dabei sind k₁ und k₂ z. B. Geschwindigkeitskonstanten der gleichen Reaktion, wobei aber die eine Komponente einmal den Substituenten (1) und das andere Mal den Substituenten (2) trägt, oder es handelt sich um die gleiche Reaktion in verschiedenen Lösungsmitteln. a und b sind experimentell festzulegende Konstanten. Analoge Beziehungen lassen sich für die Gleichgewichtskonstanten K finden. Nach dem 2. Hauptsatz der Thermodynamik ist lg K proportional zur Freien Reaktionsenthalpie, und nach der Theorie des Übergangszustandes ist lg k proportional der Freien Aktivierungsenthalpie. Deshalb stellen diese Korrelationen lineare Beziehungen zwischen Änderungen der Freien Enthalpie dar.

Eine der wichtigsten L. ist die Hammett-Gleichung (Abb.), die den Zusammenhang zwischen der Reaktionsgeschwindigkeit substituierter Benzolderivate und der Acidität der entsprechenden Benzoesäuren wiedergibt. Bedeutung erlangten auch die Edwards-Gleichung für die Geschwindigkeit nucleophiler Reaktionen, die Taft-Gleichung, die den Einfluß α-ständiger Substituenten auf die Reaktivität aliphatischer Verbindungen beschreibt, und das Brönstedtsche Katalysegesetz.