Lexikon der Geowissenschaften: Hauptkomponententransformation
Hauptkomponententransformation, Hauptachsentransformation, Verfahren der Bildverbesserung, vorrangig zur Datenreduktion ohne entscheidenden Informationsverlust. Mit der Hauptkomponententransformation wird die Abhängigkeit von Spektralbändern untereinander untersucht. Besteht eine starke Grauwertkorrelation zwischen den Spektralbändern, so liegt Redundanz vor, was in diesem Fall bedeutet, daß mehr Daten verwendet werden, als zur Übermittlung von Informationsgehalten notwendig sind. Fernerkundungsdaten liegen im allgemeinen in mehreren Spektralbändern vor und lassen sich daher als Daten in einem mehrdimensionalen Merkmalsraum (feature space) auffassen. Die Achsen dieses Raumes sind durch die Spektralbänder bestimmt. Die Lage jedes Pixels in diesem Raum wird durch seine Grauwerte in den verschiedenen Wellenlängen festgelegt. Der Gesamtdatensatz einer Szene wird sich in diesem Raum als mehr oder weniger dichter Cluster darstellen, der je nach den auftretenden Oberflächencharakteristika in kleinere, besonders dichte Subcluster zu unterteilen ist. Die Form des Clusters hängt zum einen von den Reflexionseigenschaften der abgebildeten Oberflächen ab, zum anderen von den Spektralbändern, die den Merkmalsraum aufbauen. Eine besonders wichtige Rolle spielt dabei die Korrelation zwischen diesen. Sind sie besonders hoch korreliert, so wird der Datencluster relativ eng um die Hauptdiagonale durch den Merkmalsraum (von Punkt 0,0,0 zu Punkt 255,255,255) gruppiert sein, was gleichbedeutend ist mit einer relativ geringen Informationsdichte ( Abb. 1 ). Wenn zwei Spektralbänder hoch korreliert sind, so bringt das zweite Band nur relativ wenige neue Information zur Information des ersten hinzu. Der Anteil an redundanter Information ist in diesem Fall sehr hoch. Bei Fernerkundungsdaten liegen im allgemeinen hohe Korrelationen vor, besonders innerhalb der Spektralbänder im sichtbaren Bereich, im nahen und im mittleren Infrarot. Diese hohe Korrelation erklärt sich aus den Spektraleigenschaften der Oberflächen. Somit ist zum einen die Varianz eines Spektralbandes ein Maß für seinen Informationsgehalt (sie ist ein Maß für die Streuung der Daten in diesem Band). Zum anderen ist die Kovarianz zwischen zwei Kanälen ein Maß für die Korrelation zwischen den Datensätzen und damit für den Informationsgewinn bei einer Kombination beider Spektralbänder. Hier setzt die Hauptkomponententransformation an. Über die Berechnung der Varianz-Kovarianz-Matrix eines Datensatzes wird das gesamte Koordiantensystem so gedreht, daß die neuen Koordinatenachsen jeweils in die Richtung der maximalen Streuung ( = Varianz) des Datenclusters zeigen. Dies geschieht über die Berechnung der Eigenwerte und Eigenvektoren der gegebenen Varianz-Kovarianz-Matrix. Die Grundvoraussetzung für die neuen Kanäle, die sog. Hauptkomponeneten, ist, daß sie untereinander nicht korreliert sind, d.h. ihre Kovarianz ist gleich Null. Die erste Hauptkomponente zeigt demnach in die Richtung der größten Ausdehnung des Datenclusters ( = Hauptachse eines Rotationsellipsoids); die zweite Hauptkomponente in die Richtung der zweitgrößten Ausdehnung des Datenclusters und zwar orthogonal zur Richtung der ersten Hauptkomponente. Die erste Hauptkomponente enthält somit ein Maximum an Information (sie beinhaltet die größtmögliche Varianz des gesamten Datenclusters). Die zweite Hauptkomponente bietet den statistisch größtmöglichen Informationszuwachs ( Abb. 2 und Abb. 3 ). [MN]
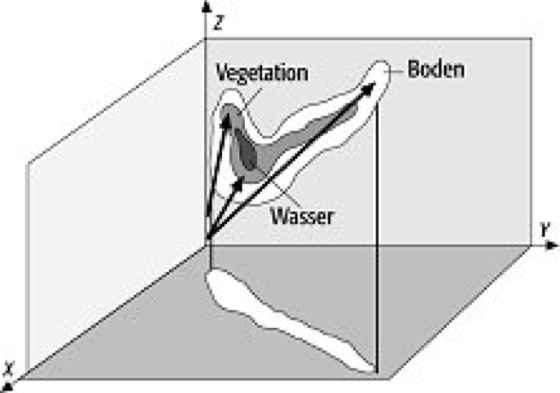
Hauptkomponententransformation 1: Datencluster einer Szene im dreidimensionalen Raum und Projektion des Clusters auf eine der Ebenen aus zwei Kanälen. Hauptkomponententransformation 1:
![](javascript:ShowPic("/lexika/images/geo/f2f742.jpg", "222", "156");)
Hauptkomponententransformation 2: Datencluster im zweidimensionalen Raum. Eingezeichnet ist eine Ellipse, die ca. 95% der Daten umfaßt. Ihre Hauptachsen entsprechen den Hauptkomponenten. Hauptkomponententransformation 2:
![](javascript:ShowPic("/lexika/images/geo/f2f743.jpg", "127", "131");)
Hauptkomponententransformation 3: Datencluster im dreidimensionalen Raum. Eingezeichnet sind die Hauptkomponenten (PC = principal components).
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.