Hemmes mathematische Rätsel: Wie lang ist die Strecke?
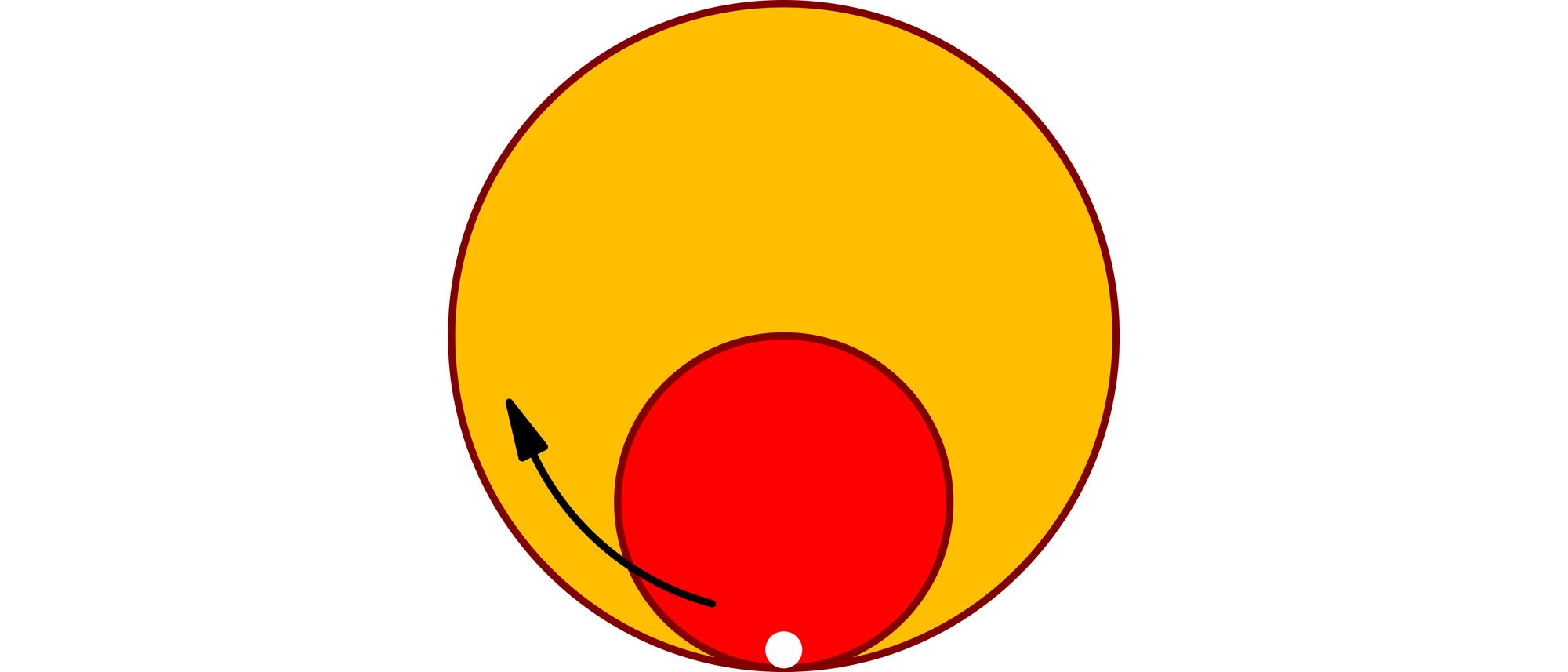
Im Inneren eines großen Kreises rollt ein kleiner Kreis ohne Schlupf auf dessen Umfang. Der Durchmesser des äußeren Kreises von einem Meter ist doppelt so groß wie der des inneren. Die Stelle, mit der der kleine Kreis zu Beginn des Rollens den großen Kreis berührt, ist mit einem weißen Punkt markiert. Wie lang ist der Weg des weißen Punktes gewesen, wenn der kleine Kreis seine Ausgangsstellung wieder erreicht?
Der Punkt auf dem Umfang des kleinen Kreises bewegt sich beim Abrollen auf dem Umfang des großen Kreises auf der Linie SS’ einmal hin und her. Sein Weg ist also 2 m lang. Um dies zu beweisen, muss man zeigen, dass für jeden beliebigen Winkel α die Bögen b1 von A nach S und b2 von A nach B gleich lang sind, denn sie werden ja aufeinander abgerollt. Die Strecken M1M2 und M2B sind beide Radien des kleinen Kreises. Das heißt, das Dreieck M1M2B ist gleichschenklig, und der Winkel an seiner Ecke B hat auch die Größe α.
Daraus ergibt sich der dritte Winkel des Dreiecks zu β = 180° − 2α und der Winkel γ zu 180° − β = 2α. Die Bögen stehen zu den Umfängen U1 und U2 des großen und kleinen Kreises im Verhältnis b1/U1 = α/360° und b2/U2 = γ/360°. Da der große Kreis doppelt so groß ist wie der kleine, kann man in der ersten Gleichung U1 durch 2U2 ersetzen. Tauscht man nun auch noch in der zweiten Gleichung γ gegen 2α aus, ergibt sich b1 = b2 = αU2/180°. Damit ist die Behauptung bewiesen.




Schreiben Sie uns!
4 Beiträge anzeigen