Stöchiometrie, die Lehre von der Berechnung der Zusammensetzung chem. Verbindungen und Mischungen sowie der Massen-, Volumen- und Ladungsverhältnisse bei chem. Reaktionen. Die Herausbildung der S. war eine wichtige Voraussetzung für die Entwicklung der Chemie zu einer exakten Wissenschaft.

Die S. basiert auf der gesicherten Erfahrung, daß bei chem. Reaktionen die chem. Elemente vollständig erhalten bleiben (Gesetz von der Erhaltung der Elemente) und die Gesamtmasse der beteiligten Substanzen konstant ist (Gesetz von der Erhaltung der Masse). Zu den eigentlichen stöchiometrischen Grundgesetzen zählen die Gesetze der stöch. Proportionen, das chem Volumengesetz von Gay-Lussac. und das Avogadrosche Gesetz. Die Grundlage für die S. von elektrochem. Vorgängen bilden die Faradayschen Gesetze, zur stöch. Berechnung von Reaktionen, an denen Gase beteiligt sind, wird die Zustandsgleichung idealer Gase benötigt.

Anwendungen. Die Anwendung der S. auf Mischungen bzw. Lösungen schließt den Umgang mit Zusammensetzungsgrößen ein. Die Durchführung stöch. Berechnungen ist in nahezu allen Teilgebieten der Chemie erforderlich. Dabei sind folgende Anwendungsfälle am häufigsten.

1) S. der Zusammensetzung von Verbindungen. Die Grundlage bilden hier die die Größen Masse m, molare Masse M und Stoffmenge n verknüpfende Gleichung M = m/n sowie die Feststellung, daß die Stöchiometriezahlen ν_i in einer Formel Stoffmengenverhältnisse angeben. So gilt z. B. für Fe₂O₃n_Fe : n_O = ν_Fe : ν_O = 2 : 3. Typische Aufgabenstellungen sind die Berechnung der Massenanteile w der einzelnen Elemente in einer Verbindung aus der Substanzformel oder die Ermittlung der Substanzformel aus den experimentell bestimmten Massenanteilen der Elemente (Elementaranalyse).

2) S. von chemischen Reaktionen. Die Berechnung des Stoffumsatzes bei chem. Reaktionen geht von der entsprechenden Reaktionsgleichung (Stoffgleichung) aus, die die stöch. Verhältnisse zwischen den Ausgangs- und Endstoffen beschreibt. Die Gleichung N₂ + 3 H₂ → 2 NH₃ gibt für den molekularen Bereich den elementaren Formelumsatz (Reaktion von einem N₂-Molekül mit drei H₂-Molekülen zu zwei NH₃-Molekülen) an und drückt gleichzeitig für den makroskopisch-stofflichen Bereich den molaren Formelumsatz (1 mol = 28,0 g N₂ reagiert mit 3 mol = 6,0 g H₂ zu 2 mol = 34,0 g NH₃) aus. Über die Beziehung m = nM kann die Umrechnung der Stoffmengen in Massen erfolgen.

Als Ausbeute einer Reaktion bezeichnet man den Quotienten aus praktisch erhaltener und theoretisch möglicher (d. h. bei vollständigem Ablauf der Reaktion gemäß ihrer S. berechneter) Menge an Endprodukt(en).

3) Herstellen, Verdünnen und Mischen von Lösungen. Lösungen bestimmter Zusammensetzung und Menge können entweder durch Auflösen der entsprechenden Substanz(en) im reinen Lösungsmittel, durch Lösungsmittelzusatz zu einer konzentrierteren Lösung (Verdünnung) oder durch Zusammengeben von Lösungen höherer und niederer Konzentration als der gewünschten (Mischen) hergestellt werden. Die stöch. Berechnungen für diese drei Methoden gehen von der Definitionsgleichung für die jeweils benutzte Zusammensetzungsgröße sowie in sehr vielen Fällen von der Beziehung m = nM aus. Beim Herstellen einer Lösung durch unmittelbares Auflösen wird die benötigte Menge der zu lösenden Substanz meist durch Wägung abgemessen. Beim Verdünnen konzentrierterer Lösungen bleiben die Stoffmenge n bzw. die Masse m der gelösten Substanz unverändert. Bezeichnet der Index 1 den Zustand vor, der Index 2 den Zustand nach dem Verdünnen, so gilt n₁ = n₂ und m₁ = m₂. Für die Stoffmengenkonzentration c bzw. den Massenanteil w gelten die für alle Verdünnungsberechnungen grundlegenden Beziehungen c₁V₁ = c₂V₂ und w₁m₁ = w₂m₂.

Für das Mischen mehrerer Lösungen (Index i) der gleichen Substanz, aber von unterschiedlicher Konzentration, gilt als Grundsatz, daß die gesamte Menge der gelösten Substanz in der Mischung (Index M) vorhanden ist:

. Die davon abgeleiteten Beziehungen

und

werden als Mischungsgleichungen bezeichnet.

4) Anwendung der S. in der quantitativen chem. Analyse. Im Falle der Gravimetrie wird der zu bestimmende Anteil durch geeignete Reaktionen und Operationen in eine stöch. wohldefinierte Wägeform Aν_A Bν_B übergeführt und deren Masse m(Aν_A Bν_B) durch Wägung bestimmt. Die in der Probe enthaltene Masse m(A) des Bestandteils A mit der Molmasse M(A) läßt sich nach

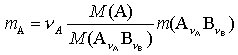
berechnen. In dieser Gleichung sind für eine gegebene gravimetrische Bestimmung die Stöchiometriezahl ν_A und die beiden Molmassen konstante Größen, die zum gravimetrischen Faktor f_grav. dieser Methode zusammengefaßt werden. Die Kenntnis der gravimetrischen Faktoren erleichtert die analytische Routinearbeit, sie sind deshalb für alle wichtigen gravimetrischen Bestimmungen in Tabellenwerken und Lehrbüchern der analytischen Chemie zusammengestellt.

In der Volumetrie geht die stöch. Auswertung einer Titration davon aus, daß bei Erreichen des Äquivalenzpunktes äquivalente Stoffmengen n_ev = nz von Titrand (Index 1) und Titrator (Index 2) miteinander reagiert haben: n_ev,1 = n_ev,2 = n₁z₁ = n₂z₂. Hierbei bedeutet z stöchiometrische Wertigkeit. Da für den Zusammenhang zwischen Stoffmenge n, Stoffmengenkonzentration c und Volumen V die Gleichung c = n/V gilt, ermöglicht die Kenntnis von c₂ und V₂ der verbrauchten Maßlösung die Berechnung des Titrandgehaltes der Probelösung: c₁ = (c₂z₂V₂)/(z₁V₁). Für die Masse an Titrand ergibt sich daraus m₁ = (M₁c₂z₂V₂)/z₁. Meist verwendet man den Titrator in Form einer Normallösung, deren Äquivalenzkonzentration n_ev,2 = n₂z₂ beträgt. Für eine gegebene titrimetrische Bestimmung und eine bestimmte Normalität der Maßlösung sind M₁, z₁ und c₂ konstante Größen, die zum titrimetrischen Faktor f_titr. = M₁c₂/z₁ zusammengefaßt werden können. Die titrimetrischen Faktoren (bisweilen auch als maßanalytische Äquivalente bezeichnet) liegen gleichfalls für wichtige maßanalytische Bestimmungen tabelliert vor. Abweichungen der Maßlösung von der angestrebten Standardnormalität (meist 0,1 N oder 0,01 N) werden bei der stöch. Auswertung dadurch berücksichtigt, daß man V₂ mit einem Korrekturfaktor, dem experimentell ermittelten Faktor F der Maßlösung, der auch als Titer bezeichnet wird, multipliziert.