azimutaler Kartennetzentwurf, E azimuthal map projection, Ergebnis eines mathematischen Verfahrens, bei dem ein Teil der Erdoberfläche durch Projektion (perspektive Entwürfe) oder durch ein anderes geometrisches Verfahren direkt in die Ebene abgebildet wird. Dabei wird oft die polare Lage, seltener die transversale und die allgemeine Lage angewendet. Die polare Lage spielt eine wichtige Rolle für die Abbildung der Polargebiete der Erde oder der scheinbaren Himmelskugel, da in der Nähe des Berührungspunktes von Kugel und Ebene die Verzerrungen am geringsten sind. Azimutale Kartennetzentwürfe sind im allgemeinen Sinne der Kartennetzentwurfslehre Kegelentwürfe mit n=1, d. h. mit einem Öffnungswinkel von 180°.
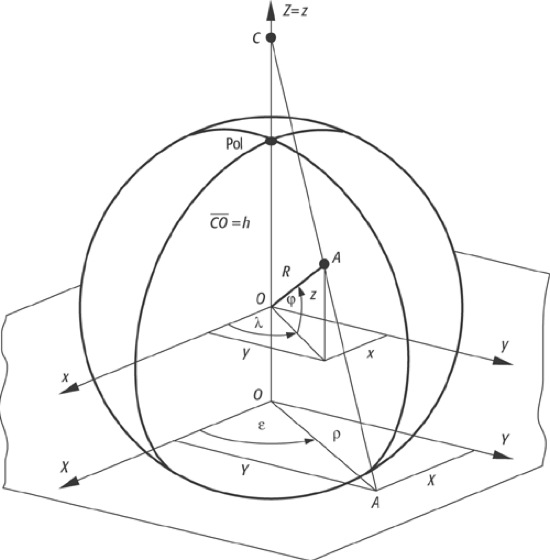
Für die azimutalen Kartennetzentwürfe, die durch Projektion entstehen, gelten die in Abb. 1 dargestellten Beziehungen für die polare Lage. In Abb. 1 sind φ und λ die geographische Breite bzw. Länge eines beliebigen Punktes A auf der Kugeloberfläche; x, y und z sind rechtwinklige Koordinaten von A auf der Kugeloberfläche. Die x,y-Ebene liegt im Äquator, die x-Achse weist in Richtung des Meridians von Greenwich, die z-Achse fällt mit der Erdachse zusammen: X und Y sind rechtwinklige Koordinaten von A′ in der Abbildungsebene. Die Orientierung der Koordinaten X, Y entspricht der der Achsen x, y, d. h., die X-Achse weist nach Norden wie in der Geodäsie. ρ und ε sind Polarkoordinaten.
Für die Zeichnung eines azimutalen Kartennetzentwurfes werden aus praktischen Gründen häufig Polarkoordinaten angewendet. Allgemein gilt das Halbmessergesetz ρ=f (φ) und für den Richtungswinkel
ε=λ.
Die wichtigsten azimutalen Kartennetzentwürfe sind: a) Orthographische Projektion. Das Projektionszentrum C liegt im Unendlichen (h=∞). Die Abbildungsgleichungen zwischen den Koordinaten x, y, z in der Bezugsfläche und X, Y in der Abbildungsebene lassen sich einfach nach dem Strahlensatz aus Abb. 1 ablesen:
X=x=R·cos φ·cos λ und
Y=y=R·cos φ·sin λ.
Halbmessergesetz: ρ=R·cos φ.
Hierbei ist R der Kugelradius. Die Verzerrungen der orthographischen Projektion lassen sich nach den Formeln für die Längen-, Flächen- und Winkelverzerrungen auf der Grundlage der Verzerrungstheorie berechnen:





Wie Abb. 2 zeigt, kann man die halbe Erdkugel in einem Kreis vom Radius R der Bezugskugel abbilden. Die Abb. 3 zeigt die Lage und Form der Verzerrungsellipsen für die polare orthographische Projektion. Die Abb. 2 und 3 machen die Stauchungen an den Kartenrändern deutlich.
Für die kartographische Abbildung von nahen Himmelskörpern (Mond, Sonne und Planeten) wird meist die orthographische Projektion in transversaler oder auch allgemeiner Lage angewendet, da die Himmelskörper wegen ihrer relativ zum Radius großen Entfernung nahezu in der orthographischen Projektion gesehen werden. Wie die Erde kann auch der Mond in orthographischer Projektion abgebildet werden. b) Gnomonische Projektion (orthodromische Projektion). Das Projektionszentrum C (Abb. 1) liegt jetzt im Kugelmittelpunkt O. Damit ist h=0, und die Abbildungsgleichungen ergeben sich zu
X=R·cot φ·cos λ,
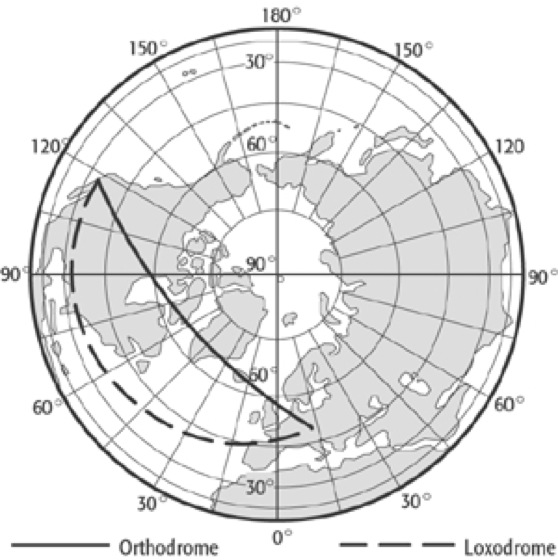
Y=R·cot φ·sin λ, das Halbmessergesetz zu ρ=R·cot φ. Die gnomonische Projektion ist der einzige Kartennetzentwurf, bei dem sind nach der jeder Orthodromenbogen (Orthodrome) auf der Kugelfläche als Gerade abgebildet wird, weil seine Ebene das Projektionszentrum enthält. Die Großkreisverbindung zwischen zwei Punkten in der Abbildungsebene lässt sich also als gerade Verbindung leicht konstruieren. Dieser Kartennetzentwurf wird für Navigationskarten angewendet. Durch punktweise Übertragung der Orthodrome in eine Navigationskarte mit anderem Kartennetzentwurf kann in letzterer der Verlauf der Orthodrome zwischen Start- und Zielort bequem graphisch ermittelt werden.
Die Formeln für die Verzerrung lassen sich aus der Verzerrungstheorie ableiten:





Für die Ränder des Entwurfs ergeben sich große Verzerrungen (Abb. 4 und 5).
c) Stereographische Projektion. Das Projektionszentrum liegt im Gegenpunkt des Tangentialpunktes 0'. Damit gilt h=R, und die Abbildungsgleichungen ergeben sich zu








mit dem Halbmessergesetz





Die stereographische Projektion ist ein winkeltreuer azimutaler Kartennetzentwurf. Nach der Verzerrungstheorie berechnet man die Verzerrungen (Tab.) des Entwurfs zu








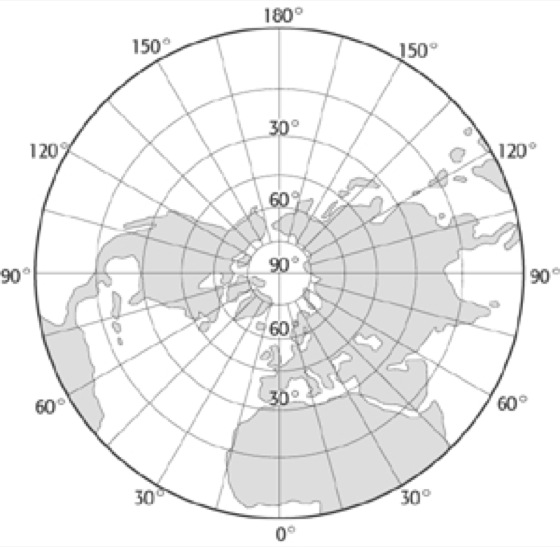
Die stereographische Projektion ist der einzige kreistreue Entwurf. Sie wird für Sternkarten bzw. -atlanten benutzt. Hipparch soll sie erstmals um 150 v. Chr. hierfür verwendet haben (Abb. 6 und 7).
d) Lamberts flächentreuer Azimutalentwurf. Da es sich hierbei nicht um eine Projektion handelt und die Forderung nach Flächentreue vorliegt, werden die Abbildungsgleichungen aus den gegebenen Verzerrungsverhältnissen abgeleitet und in Polkoordinaten angegeben. Man erhält das Halbmessergesetz ρ=2·R·sin Ψ/2, wobei Ψ=90^o-φ. Für die Winkel zwischen den Abbildungen der Meridiane gilt wie für alle azimutale Kartennetzentwürfe ε=λ.
Nach der Verzerrungstheorie erhält man








Das Kartennetz ist in Abb. 8 in polarer Lage für die Erde und in Abb. 9 in transversaler Lage für den Mond dargestellt. Dieser Entwurf bildet aufgrund seiner geringen Flächenverzerrung bei weitgehender Formtreue das Kartennetz von zahlreichen Karten in großen Weltatlanten. Wie andere flächentreue Kartennetzentwürfe ist er 1772 von J.H. Lambert angegeben worden.
e) Azimutalentwurf mit längentreuen Meridianen (mittabstandstreuer Kartennetzentwurf). Die Abbildungsgleichungen ergeben sich aus der Forderung nach längentreuen Meridianen zu ρ=R·arc Ψ, ε=λ.
Nach der Verzerrungstheorie gelten die Gleichungen








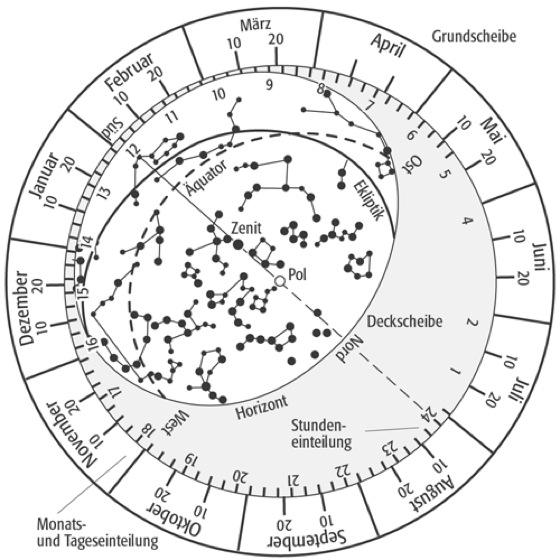
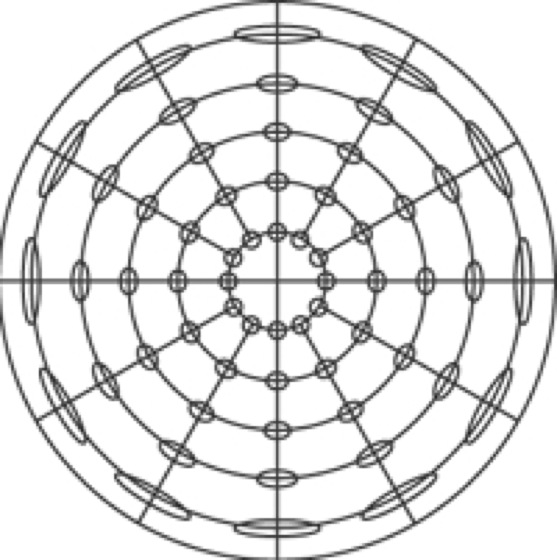
In der Regel werden eine Halbkugelfläche oder etwa 20 Breitengrade mehr abgebildet, z. B. bei der drehbaren Sternkarte (Abb. 10 ). Sie ist ein polarer Entwurf mit drehbarer Deckscheibe in allgemeiner Lage mit dem Tangentialpunkt im Zenit des betreffenden Ortes (in Abb. 10, φ=52,5°). Der Entwurf wurde 1581 von G. Postel benutzt. Eine Vorstellung von den Verzerrungen vermittelt Abb. 11 .
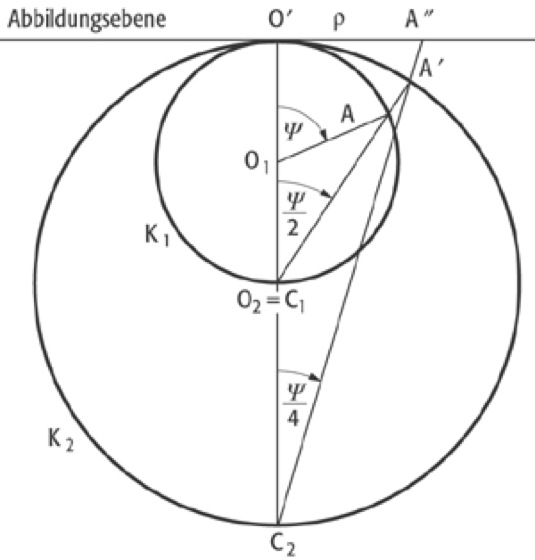
Prinzipiell kann man mit diesem Entwurf die ganze Erdoberfläche abbilden. Natürlich sind auf der Halbkugel, die der Abbildungsebene abgewandt ist, insbesondere im Gegenpol, die Verzerrungen unerträglich groß. Deshalb sind sternförmige Karten vorgeschlagen worden, die allerdings in der Gegend des Gegenpols große Klaffungen aufweisen und den Gegenpol mehrfach darstellen. Als Beispiel dient Petermanns Kartennetzentwurf (Abb. 12 ).
f) Breusings vermittelnder Entwurf. Da die stereographische Projektion an den Rändern eine starke Flächenverzerrung, der flächentreue Lambert'sche Azimutalentwurf dagegen eine starke Winkelverzerrung aufweist, schlug A. Breusing (1818-1892) als Mischkarte einen Entwurf vor, dessen Halbmessergesetz als geometrisches Mittel dieser beiden Entwürfe gebildet wird.
Stereographische Projektion:





Flächentreuer Lambert'scher Entwurf:





Für Breusings Entwurf erhält man:





wobei Ψ=90°-φ
Außerdem gilt ε=λ.
Die Berechnung der Verzerrungen wird in üblicher Weise vorgenommen und ergibt:





Die vergleichende Betrachtung der Verzerrungswerte in der Tabelle zeigt, dass der eingangs geforderte Effekt erreicht worden ist, wenngleich der Entwurf in keinem Element verzerrungsfrei ist. Er ist ein vermittelnder Entwurf.
g) Solowjows Doppelprojektion. Ein Punkt A wird zunächst stereographisch von der Kugel K₁ auf die Kugel K₂ nach A′ projiziert (Abb. 13 ). K₂ hat einen doppelt so großen Radius wie K₁. Im Tangentialpunkt der Abbildungsebene berühren sich beide Kugeln. A′ auf der Kugel K₂ wird nochmals stereographisch projiziert und in der Ebene in A'′ abgebildet. Das Halbmessergesetz lautet ρ=4·R·tan Ψ/4, ε=λ Die Verzerrungen sind nach der Verzerrungstheorie abgeleitet:








Die Möglichkeiten der Computeranwendung für Kartennetzberechnungen erweitern die Verwendung von azimutalen Kartennetzentwürfen auch auf allgemeine Achslagen. Solche Entwürfe haben den Vorteil, dass sie beim Betrachter die räumliche Vorstellung von der Gestalt der Erde besser unterstützen als die polaren und äquatorialen Achslagen. Als Beispiele hierfür sind fünf der oben behandelten Azimutalentwürfe in den Abb. 14a-e dargestellt.

KST

Literatur: [1] FIALA, F. (1957): Mathematische Kartographie. Berlin. [2] SNYDER, J.P. & VOXLAND, P.M. (1989): An Album of Map Projections. US Geological Survey Professional Paper 1453. [3] GRAFEREND, E.W. & SYFFUS, R. (1995): The oblique azimuthal projection of geodesic type for the biaxial ellipsiod: Riemann polar and normal coordinates. Journal of Geodesy Vol. 70, – Springer-Verlag. [4] BRANDENBERGER, C. (1996): Verschiedene Aspekte und Projektionen für Weltkarten. Zürich. [5] WAGNER, K. (1962): Kartographische Netzentwürfe. Mannheim.

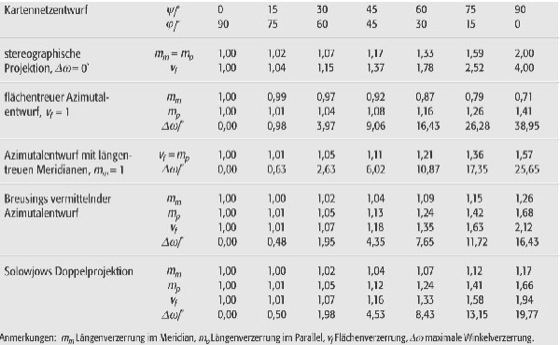
azimutaler Kartennetzentwurf (Tab):azimutaler Kartennetzentwurf (Tab): Verzerrungen.

azimutaler Kartennetzentwurf 1:azimutaler Kartennetzentwurf 1: Allgemeiner Fall eines azimutalen Kartennetzentwurfs in polarer Lage mit Projektionszentrum C auf der verlängerte Erdachse. A ist ein beliebiger Punkt der Erdoberfläche, A′ sein Bild in der Abbildungsebene.

azimutaler Kartennetzentwurf 2:azimutaler Kartennetzentwurf 2: Orthographische Projektion der Erde in polarer Lage.

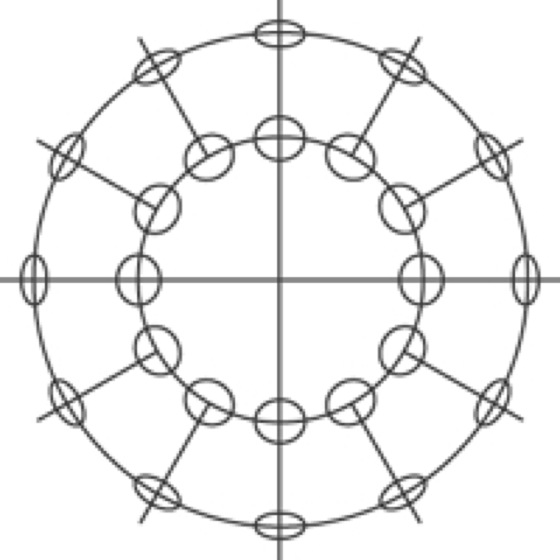
azimutaler Kartennetzentwurf 3:azimutaler Kartennetzentwurf 3: Verzerrungsellipsen der polaren orthographischen Projektion.

azimutaler Kartennetzentwurf 4:azimutaler Kartennetzentwurf 4: Gnomische Projektion der Erde in polarer Lage.

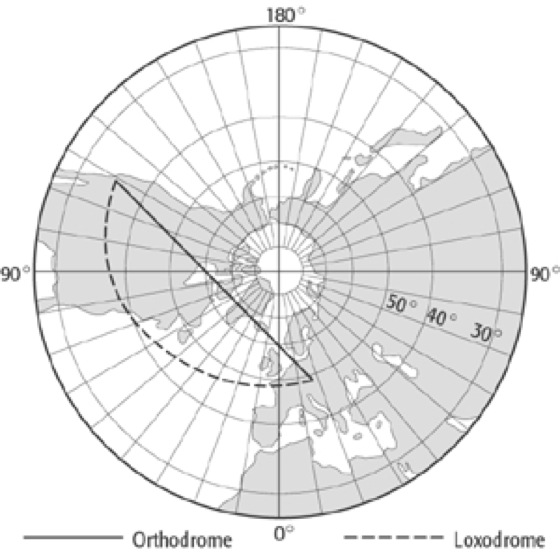
azimutaler Kartennetzentwurf 5:azimutaler Kartennetzentwurf 5: Verzerrungsellipsen der polaren gnomonischen Projektion.

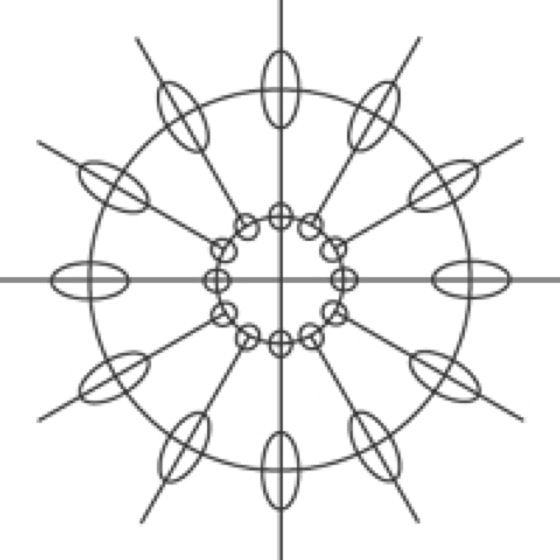
azimutaler Kartennetzentwurf 6:azimutaler Kartennetzentwurf 6: Stereographische Projektion der Erde in polarer Lage.

azimutaler Kartennetzentwurf 7:azimutaler Kartennetzentwurf 7: Verzerrungsellipsen der polaren stereographischen Projektion.

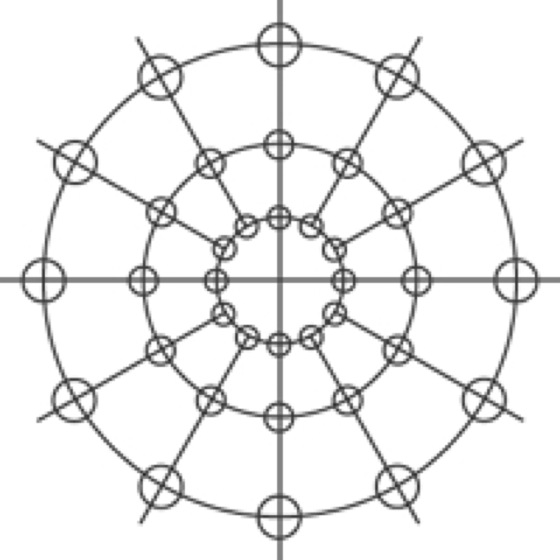
azimutaler Kartennetzentwurf 8:azimutaler Kartennetzentwurf 8: Flächentreuer Azimutalentwurf der Erde in polarer Lage.

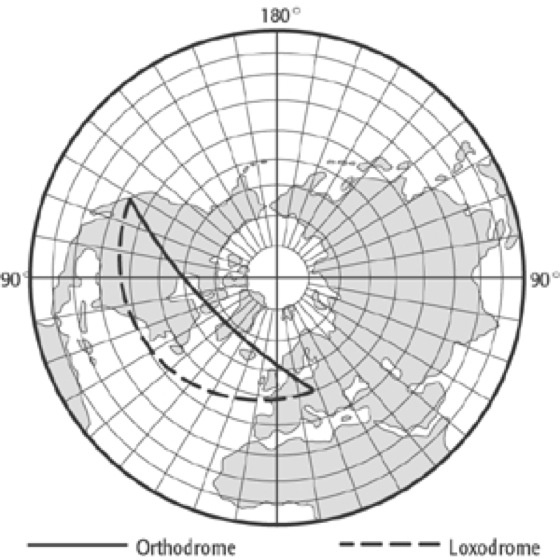
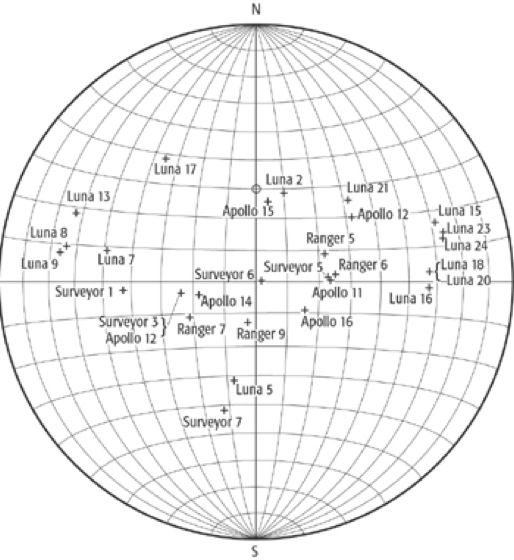
azimutaler Kartennetzentwurf 9:azimutaler Kartennetzentwurf 9: Flächentreuer Azimutalentwurf des Mondes in äquatorialer Lage mit Angabe der Landeplätze von Mondmissionen.

azimutaler Kartennetzentwurf 10:azimutaler Kartennetzentwurf 10: Drehbare Schülersternkarte.

azimutaler Kartennetzentwurf 11:azimutaler Kartennetzentwurf 11: Verzerrungsellipsen des polaren Azimutalentwurfs mit längentreuen Meridianen.

azimutaler Kartennetzentwurf 12:azimutaler Kartennetzentwurf 12: Petermanns sternförmiger Kartennetzentwurf.

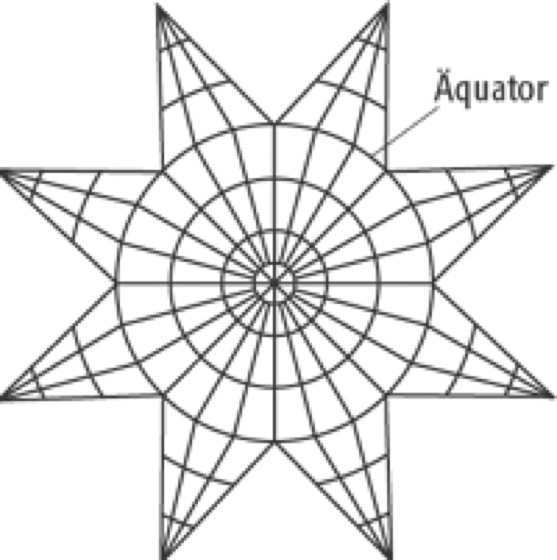
azimutaler Kartennetzentwurf 13:azimutaler Kartennetzentwurf 13: Prinzip der Doppelprojektion.

azimutaler Kartennetzentwurf 14:azimutaler Kartennetzentwurf 14: Azimutale Kartennetze in allgemeiner Lage (schiefachsige Entwürfe): a) orthographisch, b) gnomisch, c) stereographisch, d) flächentreu, e) mittabstandstreu.