Kegelentwürfe, E conical projections, Kartennetzentwürfe, bei denen als Ergebnis geometrischer Prozesse ein Teil der Erdoberfläche auf einen Kegelmantel als Zwischenabbildungsfläche abgebildet wird. Der Kegelmantel kann dann verzerrungsfrei in die Ebene (Abbildungsfläche) abgewickelt werden. Die Achse des Kegels kann mit der Erdachse unterschiedliche Winkel α einschließen (Kartennetzentwürfe; siehe dort Abb. 1). Beträgt der Winkel zwischen Kegelachse und Erdachse α = 0°, so entsteht ein Kegelentwurf in polarer oder normaler Lage, gelegentlich auch normale Abbildung genannt (Abb. 1). Für den Fall eines rechten Winkels α = 90° zwischen Erd- und Kegelachse ergibt sich ein Kegelentwurf in äquatorialer, transversaler oder querständiger Lage. Im Bereich 0° > α > 90° entsteht ein Kegelentwurf in allgemeiner Lage, d. h. ein schiefachsiger Entwurf, der für Kartennetze allerdings ohne jede praktische Bedeutung ist.
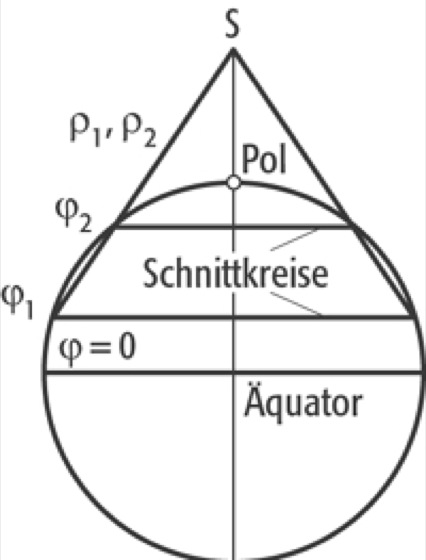
Je nach dem Öffnungswinkel des Kegels und des Abstands seiner Spitze S vom Kugelmittelpunkt werden Berührungskegel (Abb. 2), Schnittkegel (Abb. 3) und gewissermaßen über der Kugel schwebende Kegel unterschieden (Kartennetzentwürfe; Bd. 1, Abb. 2). Es ist offensichtlich, dass abzubildende Gebiete in der Nähe des Berührungskreises oder der Schnittkreise nur geringe Verzerrungen aufweisen.
Je nach den Forderungen an die Eigenschaften eines Kegelentwurfs werden geeignete Abbildungsgleichungen aufgestellt. Die jeweiligen Verzerrungen werden nach den Beziehungen der Verzerrungstheorie aus den Abbildungsgleichungen des betreffenden Entwurfs berechnet.
Bezüglich des Terminus Kegelentwürfe sei auf Abbildungsfläche verwiesen, wo der Öffnungswinkel des Kegels in den Grenzen von 0° (Zylinder) bis 180° (Ebene, azimutaler Kartennetzentwurf) liegen kann. In diesem Sinne wird ein gemeinsamer Begriff übergeordnet. Um Verwechslungen mit den eigentlichen Kegelentwürfen zu vermeiden, wird die Gesamtgruppe der Azimutal-, Kegel- und Zylinderentwürfe oft als kegelige Kartennetzentwürfe bezeichnet.
Erkennungsmerkmale eines echten Kegelentwurfs sind geradlinige Meridianbilder, die sich im Abbild S′ der Kegelspitze schneiden und in besonderen Fällen mit dem Bild des Pols zusammenfallen, sowie an den Kreisbogenstücken als Abbilder der Parallelkreise, deren gemeinsamer Mittelpunkt S′ ist. Im allgemeinen Fall ist auch das Bild des Pols ein Kreisbogenstück.
Das Prinzip der Konstruktion eines Kegelentwurfs mit Berührungskegel ist in Abbildung 2 (Schnitt durch die Kugel) und in Abbildung 4 (Ausschnitt in der Kartenebene) gezeigt.
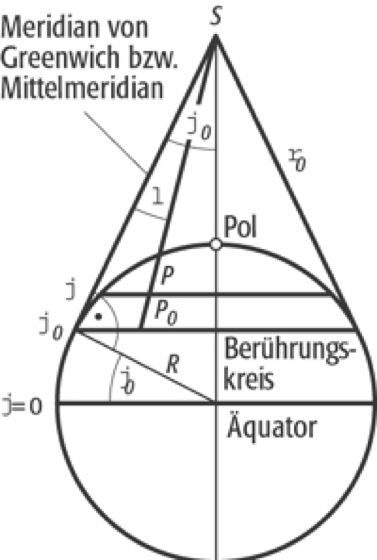
Für die Größe des Öffnungswinkels des Kegels wird ein Proportionalitätsfaktor n im Bereich 0 < n < 1 eingeführt. Die Grenzwerte n = 1 bzw. n = 0 führen auf einen Azimutalentwurf bzw. auf einen Zylinderentwurf. In Abbildung 2 ist der Schnitt eines die Kugel in der Breite φ₀ tangierenden Kegels mit der Spitze S dargestellt. Ein beliebiger Kugelpunkt P hat die geographischen Koordinaten φ und λ.
Aus Abbildung 2 kann der Abstand zwischen S und dem Breitenkreis φ₀ abgelesen werden:
ρ₀ = R · cotφ₀. (1)
In der Kartenebene (Abb. 4) wird P zu P′ mit den Koordinaten ρ und ε oder X und Y. Zwischen den Größen λ und ε besteht der erwähnte Proportionalitätsfaktor n.
Die Abbildungsgleichungen für echte Kegelentwürfe lauten in allgemeiner Form:
ρ = f (ρ₀, φ₀, φ),
ε = n · λ. (2) oder in rechtwinkligen Koordinaten (nach Abb. 4):
X = ρ₀ - ρ · cosε
Y = ρ · sinε. (3)
Je nach der Wahl der Funktion ρ = f (ρ₀, φ₀, φ) ergeben sich Kegelentwürfe mit unterschiedlichen Eigenschaften, die man entsprechend den vorgegebenen Bedingungen nach der Verzerrungstheorie festlegen kann.
Offensichtlich werden der Berührungsparallelkreis (Abb. 2) bzw. die Schnittparallelkreise (Abb. 3) bei der Abwickelung des Kegels in die Ebene verzerrungsfrei abgebildet.
Für die Längenverzerrung in den beiden Hauptrichtungen m_m (im Meridian) und m_p (im Parallelkreis) gilt allgemein nach Einführung differentieller Größen in die Abbildungen 2 und 4 sowie nach der Abbildung zur Loxodrome








Die rechte Seite für m_p ergibt sich aus der Differentiation der Gleichung (2). Wird für den Berührungsparallel in (5) ρ₀ und φ₀ eingesetzt, so ist aufgrund der erwähnten Längentreue:





und mit (1) für ρ₀ gilt:
n = sinφ₀. (6)
Der Verjüngungsfaktor n hängt also von der Breite des Berührungskreises ab. Da offensichtlich die Verzerrungen des Kartenbildes in der Nähe des Berührungsparalleles allgemein klein sind, ist es sinnvoll, φ₀ in die Mitte des abzubildenden Gebietes zu legen, insbesondere wenn dieses vornehmlich eine ausgesprochene Ost-West-Erstreckung hat.
In der Folge sollen einige Kegelentwürfe mit ihren Abbildungsgleichungen, Verzerrungsformeln und Kartennetzbildern vorgestellt werden.
1. Kegelentwurf mit längentreuen Meridianen(Abb. 5). Dieser Entwurf wurde bereits im Altertum von Ptolemäus im 2. Jh. unserer Zeitrechnung angegeben. Die Abbildungsgleichungen des Entwurfs ergeben sich aus (2) und aus der Forderung nach längentreuer Abbildung der Meridiane:
ρ = ρ₀ + R · (φ₀ - φ),
ε = n · λ (7) mit R als Erdradius im Kartenmaßstab und ρ₀ und φ im Bogenmaß. Die Verzerrungen lassen sich nach der Verzerrungstheorie berechnen.
Längenverzerrung der Meridiane: m_m = 1
Längenverzerrung der Parallele und Flächenverzerrung:





Winkelverzerrung:





2. Schnittkegelentwurf mit längentreuen Meridianen. Dieser wahrscheinlich von de l'Isle (1745) angegebene Entwurf hat zwei längentreue Parallelkreisabbilder (Abb. 3). Die Abbildungsgleichungen lauten nach den vorgegebenen Bedingungen:
ρ = ρ₀ + R · (φ₀ - φ),
ε = n · λ. (8)
ρ₀ hat hier im Gegensatz zum Ptolemäischen Entwurf keine anschauliche Bedeutung. Vielmehr wird





mit





Im Zähler sind φ₀, φ₁ und φ₂ im Bogenmaß einzusetzen. Ergebnis für den Proportionalitätsfaktor ist:





wo jetzt die Größen im Nenner im Bogenmaß stehen.
3. Flächentreuer Kegelentwurf(Abb. 6), von J. H. Lambert 1772 erstmals verwendet. Nach der Verzerrungstheorie muss das Produkt aus Längenverzerrung im Meridian m_m und im Parallelkreis m_p gleich 1 sein (vgl. Gleichungen (4) und (5)):





Die Trennung der Variablen ergibt die Differentialgleichung:





Nach allgemeiner Integration folgt:





und für den Berührungsparallel φ₀ entsprechend:





Die Subtraktion dieser Gleichung von der vorigen ergibt eine Beziehung für ρ. Damit sind die vollständigen Abbildungsgleichungen für den Lambert'schen flächentreuen Kegelentwurf:





mit den charakterisierenden Hilfsgrößen
ρ₀ = R · cotφ₀ und n = sinφ₀.
Zur Berechnung der Verzerrungen erhält man





4. Flächentreuer Schnittkegelentwurf(Abb. 7), von H.C. Albers 1805 eingeführt. Die Längenverzerrungen der Bilder der Meridiane und Parallelkreise sind kleiner als beim vorher behandelten Lambert'schen Entwurf. Diesen Vorteil erreichte Albers durch Verwendung zweier längentreuer Parallelkreise (vgl. Abb. 3), also eines Schnittkegels. In Abbildung 7 sind die Parallelkreise φ₁ = 35° und φ₂ = 65° verwendet worden. Die Abbildungsgleichungen unterscheiden sich nicht von den in den Gleichungen (9) genannten, aber die charakterisierenden Konstanten sind wesentlich komplizierter zu berechnen:





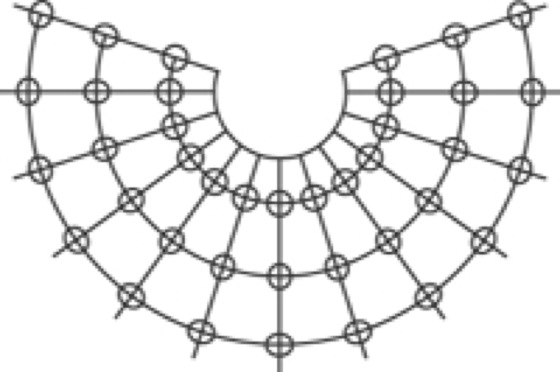
Der Vergleich der Verzerrungswerte m_m und m_p der flächentreuen Kegelentwürfe von Lambert und Albers, zeigt deutlich den Vorteil des Schnittkegels bei Albers. Die Stärke des Schnittkegels zeigt sich auch in den Verzerrungsellipsen, die in Abbildung 8 für den Albers-Entwurf dargestellt sind und vom Nordpol bis zum Äquator nahezu kreisförmig sind, was auch zu kleineren Winkelverzerrungen gegenüber dem Lambert-Kegelentwurf führt.
Diese günstigen Eigenschaften führen dazu, dass der von Albers angegebene flächentreue Schnittkegelentwurf in Atlaswerken weithin angewendet wird.
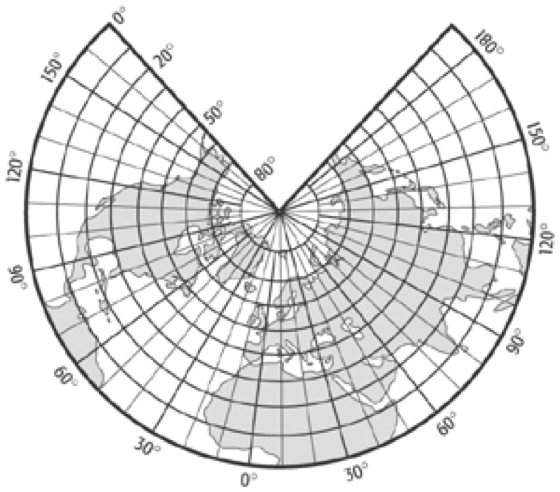
5. Winkeltreuer Kegelentwurf(Abb. 9), von J.H. Lambert 1772 erstmals verwendet. Die Winkeltreue bzw. Konformität wird erreicht, wenn die Längenverzerrungen m_α von einem bestimmten Punkt aus in allen Richtungen gleich groß sind. Damit gilt auch m_m = m_p (Verzerrungstheorie). Für Kegelentwürfe mit Berührungskegel bedeutet das mit den Gleichungen (4) und (5):





Resultat der Trennung der Variablen, Integration und Festlegung der Integrationskonstanten ist die Abbildungsgleichungen des Kartennetzes:





worin ρ₀ = R · cotφ₀ und n = sinφ₀ ist.
Die Verzerrungen sind:





und





Vergleiche auch die Verzerrungswerte in der Tabelle.
Über unechte Kegelentwürfe s. Bonnes unechter Kegelentwurf und polykonischer Entwurf.

KST

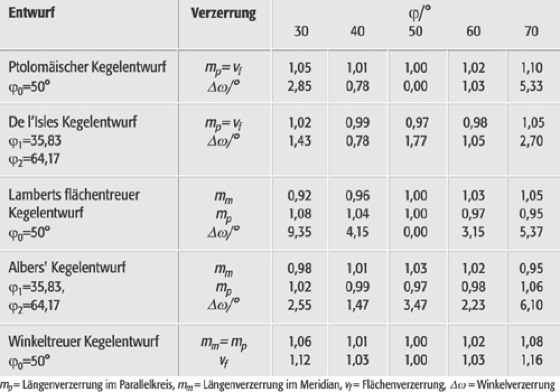
Kegelentwürfe (Tab.):Kegelentwürfe (Tab.): Verzerrungen bei Kegelentwürfen (nach Fiala).

Kegelentwürfe 1:Kegelentwürfe 1: Prinzip der Kegelentwürfe.

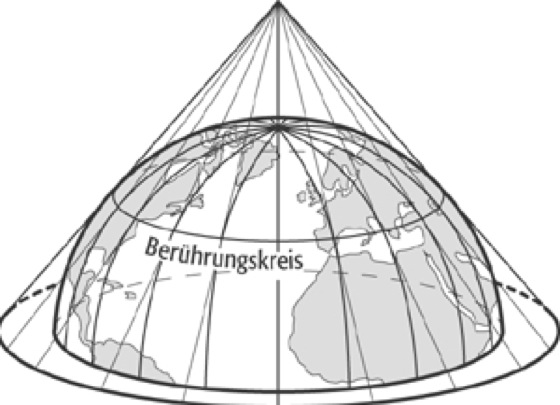
Kegelentwürfe 2:Kegelentwürfe 2: Berührungskegel als Zwischenabbildungsfläche.

Kegelentwürfe 3:Kegelentwürfe 3: Schnittkegel als Zwischenabbildungsfläche.

Kegelentwürfe 4:Kegelentwürfe 4: In die Abbildungsebene abgewickelter Berührungskegel.

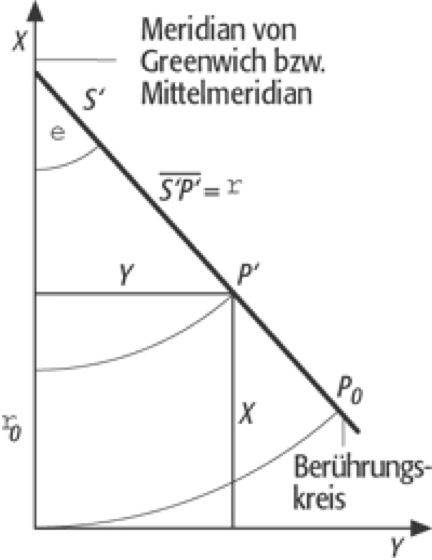
Kegelentwürfe 5:Kegelentwürfe 5: Ptolemäischer Kegelentwurf (φ₀ = 50°).

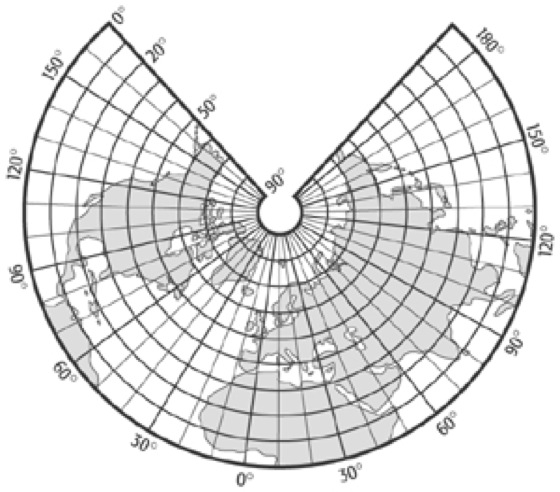
Kegelentwürfe 6:Kegelentwürfe 6: Lamberts flächentreuer Kegelentwurf (φ₀ = 50°).

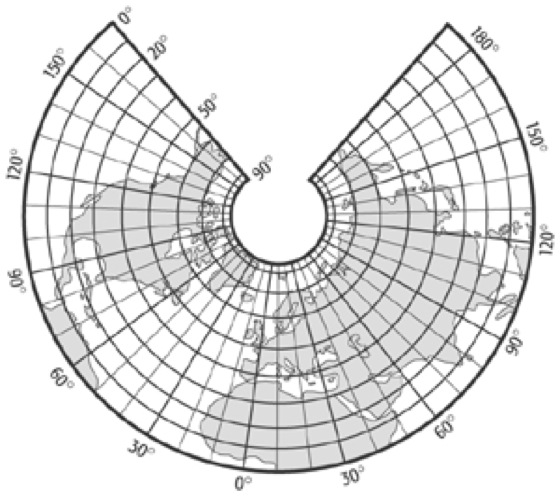
Kegelentwürfe 7:Kegelentwürfe 7: Albers' flächentreuer Schnittkegelentwurf.

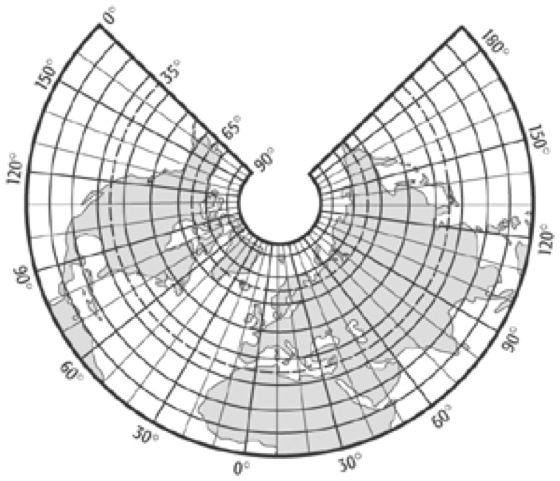
Kegelentwürfe 8:Kegelentwürfe 8: Verzerrungsellipsen für Albers flächentreuen Schnittkegelentwurf zwischen Nordpol und Äquator.

Kegelentwürfe 9:Kegelentwürfe 9: Lamberts winkeltreuer Kegelentwurf (φ₀ = 50°).