Lexikon der Kartographie und Geomatik: Kartennetzentwürfe
Kartennetzentwürfe, im mathematischen Sinn Sonderfälle der Abbildung der Koordinatennetze zweier beliebiger Flächen aufeinander. Ein gewählter Entwurf ist die mathematische Grundlage für eine analoge Karte bzw. ein digitales Kartenmodell unterschiedlicher Zweckbestimmung. Kartennetzentwürfe umfassen den Sonderfall der Abbildung des Systems der geographischen bzw. geodätischen Koordinaten (Länge λ und Breite φ) der Bezugsfläche (Erdellipsoid, Erdkugel) in die Abbildungsfläche (Globus oder Kartenebene). Sie bilden die Grundlage von Karten im Maßstab 1 : 500 000 und kleiner und werden verschiedentlich auch als kartographische Abbildungen im engeren Sinne bezeichnet. Dabei beruht der verwendete Kartennetzentwurf auf eindeutigen differenzierbaren Funktionalbeziehungen zwischen Urbild (Bezugsfläche) und Abbildung. Diese Bedingung müssen die Abbildungsgleichungen erfüllen. Die Abbildung des Erdkörpers in die Ebene unterliegt Verzerrungen (Verzerrungstheorie). Es treten Längenverzerrungen, Flächenverzerrungen und Azimut- bzw. Winkelverzerrungen auf, die durch die Gestaltung der Abbildungsgleichungen für den Zweck der jeweiligen Karte minimiert werden. Kartennetzentwürfe, die die genannten Verzerrungen nicht aufweisen, sind längentreu (gilt nur entlang bestimmter Linien oder in differentiellen Bereichen; Längentreue), flächentreu (Flächentreue) oder winkeltreu (Winkeltreue). Für viele Zwecke sind Kartennetzentwürfe zweckmäßig, die zwar in keinem der genannten Elemente verzerrungsfrei sind, dafür aber insgesamt sehr geringe Verzerrungen aufweisen. Sie werden als vermittelnde Kartennetzentwürfe bezeichnet. Diese Gruppe gewinnt zunehmend an Bedeutung, da die komplizierten Abbildungsgleichungen eines vermittelnden Kartennetzentwurfes bei Computeranwendung kein Hindernis mehr darstellen.
Geometrisch betrachtet kann die Gruppe von Kartennetzentwürfen, die das Ergebnis geometrischer Konstruktionen sind, als Kegelentwürfe bezeichnet werden. Hierbei werden Kegel mit Öffnungswinkeln α im Bereich 0° > α > 180° verwendet. In den Grenzfällen α = 0° wird aus dem Kegel direkt eine Ebene, für α = 180° ein Zylinder. Kegel und Zylinder können dann ohne weitere Verzerrungen in die Ebene abgewickelt werden. Für die Einordnung und Systematisierung der Kartennetzentwürfe ist von Bedeutung, wie die Erdachse und die Achse des Abbildungskegels zueinander liegen. Man unterscheidet eine a) polare, auch polständige oder normale, b) äquatoriale, auch äquatorständige oder transversale, und c) allgemeine, auch schiefachsige Lage der Kegelachse, die mit der Erdachse den Winkel α einschließt (Abb. 1 ). Schließlich ist noch zu unterscheiden, ob der Kegel die Bezugsfläche berührt, schneidet oder weder berührt noch schneidet (Abb. 2 ).
Kartennetzentwürfe, denen ein Kegel, in welcher Form und in welcher Lage auch immer, zugrunde liegt, heißen echt kegelige Kartennetzentwürfe. Kartennetzentwürfe, deren Konstruktion auf Abbildungsgleichungen beruht, die eine Minimierung der Verzerrungen erreichen und dabei auch dem räumlichen Vorstellungsvermögen des Benutzers entgegenkommen, heißen unecht kegelige Kartennetzentwürfe. Einige Eigenschaften echt und unecht kegeliger Kartennetzentwürfe in polarer Lage sind in der Tabelle für die Hauptkugelkreise und die Winkel θ zwischen ihnen dargestellt.
Theoretisch ist eine unbegrenzte Zahl von Kartennetzentwürfen möglich. Etwa 400 Entwürfe sind ausgearbeitet worden, wovon weniger als 50 tatsächlich verwendet worden sind. Eine wichtige Rolle bei der Entwurfswahl spielt die Größe des zu kartierenden Gebietes. Für große Gebiete in einem kleinen Maßstab gelten die elementaren Regeln: a) für eine Karte der polaren Gebiete ist ein azimutaler Kartennetzentwurf zu verwenden, b) zur Darstellung eines Gebietes in mittleren Breiten ist ein Kegelentwurf günstig, c) eine sich um den Äquator erstreckende Zone wird zweckmäßig mittels eines Zylinderentwurfs abgebildet. Diese drei einfachen Regeln werden durch die Hinzunahme von Kartennetzen in allgemeiner und transversaler Lage erweitert. Vereinfacht ausgedrückt kann man ein kreisähnliches Gebiet günstig in einem Azimutalentwurf in beliebiger Lage darstellen. Langgestreckte Gebilde werden günstig auf einen schiefen Kegel- oder Zylindermantel abgebildet, dessen Berührungskreis mit der Kugel etwa durch die Mitte des betreffenden Gebietes verläuft.
Weitere Auswahlkriterien sind durch die Verzerrungsverhältnisse gegeben. Als Faustformel kann die von Young (1920) angegebene Regel gelten: Ist z auf dem Globus die größte Winkeldistanz von der Mitte eines unsymmetrischen Gebietes bis zum entferntesten Punkt und δ seine Breite (z. B. der Winkel zwischen zwei Parallelkreisen), dann empfiehlt Young für einen Quotient z/δ > 1,41 einen Azimutalentwurf. Ist diese Zahl größer als der kritische Wert 1,41, erweist sich ein Kegelentwurf als vorteilhafter. Ginzburg und Salmanova erhielten drei kritische Werte z/δ in Abhängigkeit von den speziellen Eigenschaften: Für die Bereiche 0° > z > 25° und 0° > δ > 35° und unter Einschluss der Zylinderentwürfe sind dies konforme Entwürfe z/δ = 1,41, äquidistante Entwürfe z/δ = 1,73 und flächentreue Entwürfe z/δ = 2,00.
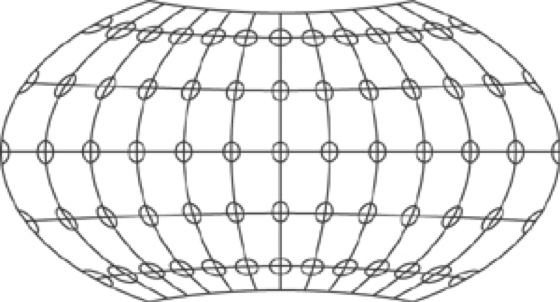
Für Weltkarten in einem Blatt erweisen sich die echten Zylinderentwürfe in polarer Lage zunächst als anwendbar. Sie erfüllen jedoch die wichtige Forderung nach Formtreue sehr schlecht und haben in den polaren Gebieten unerträgliche Verzerrungen. Deshalb ist viel Mühe auf die Entwicklung unechter Zylinderentwürfe gelegt worden. Der Dumont Weltatlas (1997) verwendet für globale Übersichtsdarstellungen den Entwurf Wagner VII, einen modifizierten Azimutalentwurf (Abb. 3 und 4). Einzelne Länder oder Gruppen von Ländern sowie Kontinente werden dort in der Mehrzahl in Lamberts konformem Kegelentwurf, kompakte Länder in Lamberts flächentreuem Azimutalentwurf dargestellt.
Zur Verbesserung der Verzerrungseigenschaften eines Kartennetzentwurfs werden die geringen Verzerrungen in einem Teil des Kartenentwurfs (in der Nähe des Berührungspunktes oder -kreises der Abbildungsfläche) auf einen größeren Teil der abzubildenden Fläche erweitert. Das geschieht im wesentlichen durch Multiplikation der Koordinatenwerte des Gebietes geringerer Verzerrungen mit geeigneten Faktoren. Die quadratische Plattkarte (Zylinderentwürfe) besitzt für den Radius R = 1 die einfachen AbbildungsgleichungenX = φ und Y = λ. Mittels der Faktoren m und n wird daraus:
X' = m · φ und Y' = n · λ.
Soll z. B. die Abbildung nach Nord und Süd auf die Parallelkreise 75° gestaucht werden, so erhält m den Wert m = 0,83. Entsprechendes gilt für n. Eindrucksvolle Beispiele für die Vielzahl der durch Umbeziffern entstandenen Entwürfe sind Aïtow-Hammers flächentreuer Entwurf und der modifizierte Entwurf Wagner VII.
KST
Literatur: MALING, D.H. (1992): Coordinate Systems and Map Projections. Pergamon Press.
Kartennetzentwürfe (Tab.):Kartennetzentwürfe (Tab.): Eigenschaften echt und unecht kegeliger Kartennetzentwürfe in polarer Lage.
![](javascript:ShowPic("/lexika/images/karto/tkartnet.jpg", "300", "170");)
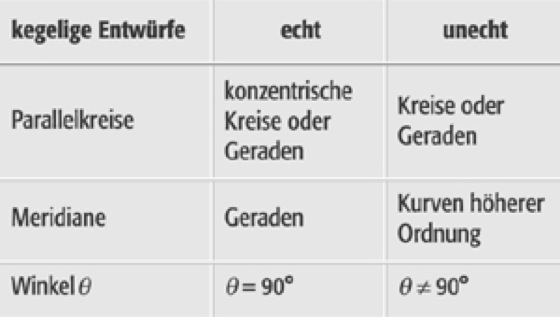
Kartennetzentwürfe 1:Kartennetzentwürfe 1: Lage der Kegelachse.
![](javascript:ShowPic("/lexika/images/karto/kartenn1.jpg", "200", "631");)
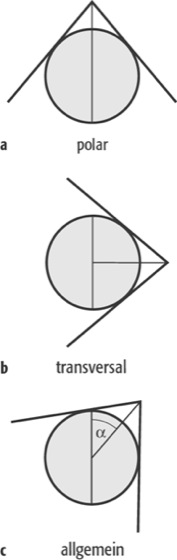
Kartennetzentwürfe 2:Kartennetzentwürfe 2: Form des Kegels.
![](javascript:ShowPic("/lexika/images/karto/kartenn2.jpg", "200", "575");)
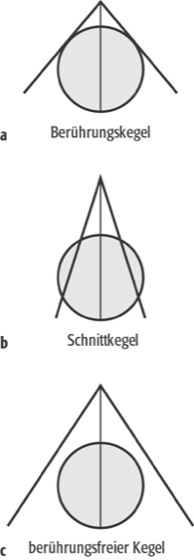
Kartennetzentwürfe 3:Kartennetzentwürfe 3: modifizierter Azimutalentwurf VII von Wagner.
![](javascript:ShowPic("/lexika/images/karto/kartenn3.jpg", "500", "270");)
Kartennetzentwürfe 4:Kartennetzentwürfe 4: Verzerrungsellipsen zum Azimutalentwurf VII von Wagner.
![](javascript:ShowPic("/lexika/images/karto/kartenn4.jpg", "300", "162");)
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.