Fizeau-Interferometer, Interferometer mit reellem Keil, der von einer Referenz- und einer Prüflingsfläche gebildet wird. F. werden hauptsächlich für die Prüfung von ebenen und sphärischen Flächen eingesetzt. Abb. 1 gibt den Strahlengang in einem Plan-F. wieder. Das quasimonochromatische Licht einer Spektrallampe oder eines Lasers dient zur Beleuchtung der zwei Planflächen A und B. Der Kollimator erzeugt eine Planwelle, die nahezu senkrecht auf die Planflächenkombination trifft. Das von den Flächen A, B reflektierte Licht wird über einen Spiegel in der Umgebung des Fokus des Kollimators auf eine Blende gelenkt, die die Reflexe von den Rückseiten von Referenz- und Prüflingsfläche weglenkt. Durch diese Blende hindurch wird die Flächenkombination A, B mit einer Kamera abgebildet. Da die Interferenzerscheinung am Orte der Platten lokalisiert ist (Lokalisationsbereich von Interferenzmustern), hat das Interferenzbild den höchsten Kontrast nur bei dieser Art der Abbildung. Die Flächen A, B lassen sich nur paarweise prüfen. Im allgemeinen ist B eine Normalfläche hinreichender Güte.

Abb. 2 zeigt eine Anordnung zur Prüfung von sphärischen Flächen. Während bei Planflächen eine ebene Welle zur Beleuchtung verwendet wird, benutzt man im Falle sphärischer Flächen sphärische Wellen, die überall senkrecht auf die Testfläche einfallen. Als Referenzflächen werden komplementär gekrümmte Sphären verwendet. Die Dicke des Luftspaltes zwischen Referenz- und Prüflingsfläche ist gleich der Radiendifferenz. Bei Einhaltung guter sphärischer Korrektur des Interferometers und Erfüllung der Sinusbedingung lassen sich auch größere Radiendifferenzen tolerieren. Das setzt im allgemeinen aber Laser-Beleuchtung voraus. Gestrichelt ist ein alternativer Strahlengang zur Prüfung konkaver Sphären angegeben. Damit die Korrektionsbedingungen für das Interferometer eingehalten werden, müssen die Referenzflächen entweder als konzentrische oder als aplanatische Menisken ausgelegt sein.

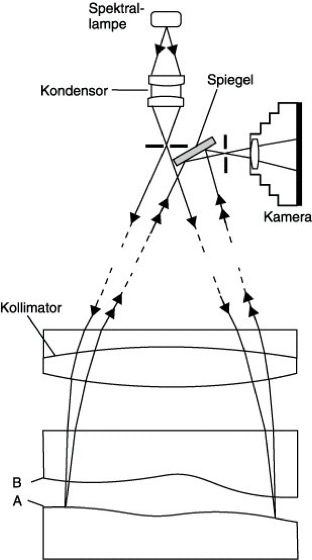
Fizeau-Interferometer 1: Anordnung zur Prüfung ebener Flächen.

Fizeau-Interferometer 2: Anordnung zur Prüfung sphärischer Flächen.