Lexikon der Physik: Energiesatz
Energiesatz, Energieprinzip, Satz oder Prinzip von der Erhaltung der Energie, uneingeschränkt gültiges, grundlegendes Prinzip, dem zufolge bei keinem physikalischen Vorgang Energie vernichtet oder erzeugt, sondern nur von einer Form in eine andere umgewandelt werden kann.
In einem abgeschlossenen System ist demnach die Gesamtenergie, die sich aus Energien in verschiedensten Erscheinungsformen wie Wärme, Licht, chemische Affinität, Elektrizität, Magnetismus oder Masse etc. zusammensetzen kann, eine absolute Erhaltungsgröße, wohingegen jede einzelne dieser Energien eines Systems für sich nicht erhalten sein muß. Soll die Gesamtenergie um einen bestimmten Betrag erhöht werden, so muß dieser Energiebetrag von außen zugeführt werden, so daß das System dann zumindest vorübergehend nicht mehr als abgeschlossen gelten kann. Gibt ein System ein Quantum Energie ab, so sinkt seine Gesamtenergie um eben dieses Quantum; ein Perpetuum mobile erster Art ist daher unmöglich.
Betrachtet man das Weltall als abgeschlossenes System, so kann man den Energiesatz auch in folgender Form aussprechen: Der Gesamtvorrat des Weltalls an Energie ist unveränderlich.
Schon Huygens (1673) und insbesondere Leibniz, letzterer zunächst auf der Basis metaphysischer Betrachtungen zur Unveränderlichkeit Gottes, von denen er im Laufe der Zeit zu einer fest umrissenen physikalischen Konzeption gelangte, beschäftigten sich mit dem Energiesatz; Leibniz erkannte bereits, daß die ›force vive absolue‹ (die Gesamtenergie) als Summe von vis viva (kinetischer Energie) und potentia agendi (potentieller Energie) erhalten bleibt. Der Energiesatz in allgemeinerer Form wurde von R. Mayer (1842) und H. Helmholtz (1847) formuliert. Mayer beschränkte seine Überlegungen im wesentlichen auf die mechanische Energie und die Wärme, die er als Energieform erkannte, wobei sein besonderes Verdienst darin liegt, daß es ihm gelang, als erste wesentliche experimentelle Bestätigung des Energieprinzips einen Wert für das mechanische Wärmeäquivalent, also den Umrechnungsfaktor zwischen mechanischer und Wärmeenergie, zu ermitteln. Helmholtz erweiterte in seiner Abhandlung ›Über die Erhaltung der Kraft‹ den Energiesatz auf alle damals bekannten Energieformen. J. P. Joule konnte in der Zeit zwischen 1842 und 1850 in systematischen Versuchen die Existenz des mechanischen Wärmeäquivalents bestätigen und bereits einen sehr genauen Wert dafür ermitteln. Spätestens damit war es möglich, den Energiesatz als ein empirisch-nachprüfbares Faktum in die Wissenschaft zu integrieren. Bei seiner letzten großen Prüfung im Rahmen der Quantentheorie hat das Energieprinzip seine volle Gültigkeit behalten; Annahmen, wie sie von Bohr und anderen in den zwanziger Jahren gemacht wurden, daß die in der Heisenbergschen Unschärferelation zum Ausdruck kommende prinzipielle Unschärfe der Energie den Schluß erlaube, die Energieerhaltung gelte nur statistisch im zeitlichen Mittel, konnten widerlegt werden.
Im Rahmen des Noether-Theorems, das raumzeitliche Symmetrieeigenschaften des betrachteten Systems mit erhaltenen Größen verknüpft, kann die Energieerhaltung auf die Homogenität der Zeit zurückgeführt werden; die Energie stellt in diesem Sinne eines der sieben Bewegungsintegrale der Mechanik dar. Es kann dies zwar nicht als Beweis des Energiesatzes in seiner ganzen umfassenden Bedeutung für die gesamte Physik verstanden werden, bis heute ist aber keine einzige physikalische Erfahrung gemacht worden, die der Energieerhaltung widerspricht. Dies hat dazu geführt, daß der Energiesatz in der physikalischen Theorienbildung häufig die Rolle eines Satzes a priori einnimmt, eines Satzes also, der unabhängig von der Erfahrung als notwendige Eigenschaft einer neuen Theorie gefordert wird.
Die Formulierung des Energiesatzes unterscheidet sich in den verschiedenen Gebieten der klassischen und modernen Physik; dabei spielt die historische Entwicklung des jeweiligen Gebietes ebenso eine Rolle wie die Frage, welche Energieformen (Energie) in dem jeweiligen Bereich von Relevanz sind.
Der mechanische Energiesatz (mechanische Energie), aus dem der allgemeine Energiesatz später hervorgegangen ist, lautet: Die Summe der kinetischen Energie T und potentiellen Energie V ist konstant in Systemen, die entweder abgeschlossen oder nur konservativen Kräften unterworfen sind:
Der absolute Wert der Gesamtenergie ist nur bis auf eine beliebige additive Konstante bestimmt, die meist so fixiert wird, daß die Energie eines freien ruhenden Körpers verschwindet. Von Reibung, durch die mechanische Energie in Wärmeenergie übergeht, wird abgesehen (sog. reine Mechanik). Anderenfalls, wenn also nichtkonservative äußere Kräfte auftreten oder nicht eigentlich mechanische Phänomene wie Reibung oder Wärme zu berücksichtigen sind, gilt der Energiesatz der reinen Mechanik nicht mehr.
In der Thermodynamik und statistischen Mechanik, in der das Energieprinzip, der Namensgebung durch Clausius folgend, als erster Hauptsatz der Thermodynamik formuliert wird, müssen Energieformen berücksichtigt werden, die wie z.B. die Wärme auf der statistischen Natur der betrachteten Phänomene beruhen, letzlich aber im Rahmen der kinetischen Wärmetheorie begrifflich auf die mechanischen Energien zurückgeführt werden können.
In den klassischen Feldtheorien, also der Elektrodynamik und der in der Allgemeinen Relativitätstheorie formulierten Theorie der Gravitation, wird eine neue Qualität der Energie eingeführt, indem nicht nur massebehafteten Objekten, sondern auch den immateriellen Feldern Energie zugesprochen wird, die über den von den Feldern eingenommenen Raum kontinuierlich verteilt ist. In der Praxis führt man den Begriff einer räumlichen Dichte der Energie ein. Mit diesem Begriff kann man den Energiesatz in der klassischen Feldphysik so formulieren: In einem abgeschlossenen Raum, dem Energie weder zugeführt noch entzogen wird, ist das Integral über die Energiedichte konstant. Wandert Energie aus dem Raumgebiet zu oder ab, so ist die Änderung des Energieinhaltes gleich ihrem Strom durch die Oberfläche. Die Energie wird also wie strömende Materie in der Gas- oder Hydrodynamik behandelt.
In der Speziellen Relativitätstheorie tritt der Energiesatz in der modifizierten Gestalt

oder als
auf. Als eine völlig neue Form der Energie wird hiermit die Ruhenergie erkannt, der Energieinhalt eines ruhenden freien Körpers also, der gemäß der bekannten Formel ![]()
mit der Masse des Körpers identifiziert werden kann. Im Gegensatz zur nichtrelativistischen Physik ist damit auch der Absolutwert der Energie in einem bestimmten Bezugssystem festgelegt. Der separate Erhaltungssatz für die Masse gilt nun jedoch nicht mehr, da die Masse als eine den anderen Energiearten äquivalente Erscheinungsform auch in diese umgewandelt werden kann. Diese Umwandlung kann beispielsweise bei der Paarerzeugung oder -vernichtung von Elementarteilchen beobachtet werden, bei der Energie ›materialisiert‹ bzw. Masse ›zerstrahlt‹ wird. Ähnliches tritt bei der Masse eines zusammengesetzten Partikels auf, z.B. bei der eines Atoms, die meist nicht gleich der Summe der Massen seiner Konstituenten ist; dies hat seine Begründung darin, daß die Energie, die den Massen der freien Konstituenten entspricht, gleich derjenigen sein muß, die sich aus der der Masse des Atoms entsprechenden Ruhenergie zuzüglich der Bindungsenergie, die die Bestandteile zusammenhält, zusammensetzt: 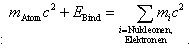
. Dieses Phänomen wird als Massendefekt bezeichnet.
Im Rahmen der Quantentheorie ist der Energiesatz nochmals überdacht worden. Die Energie wird hier, gleich den anderen physikalischen Größen, nicht mehr wie in der klassischen Physik als eine Funktion der Koordinaten und der Zeit begriffen, sondern als ein Operator, der Hamilton-Operator, der auf die Zustände eines abstrakten Hilbert-Raums wirkt; die Energiewerte ergeben sich als Eigenwerte dieses Operators. In sogenannten nichtstationären Systemen, bei expliziter Zeitabhängigkeit der betrachteten Prozesse also, so z.B. bei einem Streuprozeß, ist die Energie mit einer prinzipiellen Unsicherheit behaftet. Es gilt die Unbestimmtheitsrelation ![]()
. Je kleiner das Zeitintervall Δt, das zur Messung des Energieinhalts eines Systems zur Verfügung steht, um so größer ist die Ungenauigkeit, mit der die Energie bestimmt ist. Es kann nun zu scheinbaren Verletzungen des Energiesatzes kommen. Beim sogenannten Tunneleffekt beispielsweise gelingt es einem Teilchen, ein Hindernis zu ›durchtunneln‹, das es nach der klassischen Physik aus Energiegründen nicht überwinden könnte. Das Hindernis muß dazu nur so schmal sein, daß die kurze Zeit, die das Teilchen sich in dem Hindernis befindet, nicht ausreicht, um die Energie genauer festzulegen als bis auf den Energiebetrag, der zur Überwindung des Hindernisses nach der klassischen Physik notwendig ist. Ein anderes Beispiel für die scheinbare Verletzung des Energiesatzes in der Quantenmechanik sind die bei Streuprozessen von Elementarteilchen kurzzeitig auftretenden virtuellen Zwischenzustände, deren Energie höher sein kann als der Energieübertrag des Stoßes. Solche Phänomene könnten den Gedanken nahelegen, daß der Energiesatz in der Mikrophysik überhaupt nur im statistischen Mittel gilt. Diese Vermutung ist von Bohr, Kramers und Slater 1924 und nochmals 1929 von Bohr zur Erklärung des scheinbaren Energiedefizits beim atomaren Betazerfall ausgesprochen worden. Experimentell hat sich jedoch erwiesen, daß in jedem Fall, in dem die Energie einen genau definierten Wert annimmt, diese Energie auch exakt erhalten bleibt. Da weiterhin im Rahmen der Kopenhagener Interpretation der Quantenmechanik die Unbestimmtheit der Energie nicht etwa als der Ausdruck dessen angesehen wird, daß der eigentlich durchaus wohldefinierte Wert der Energie lediglich aus welchen Gründen auch immer nicht bekannt ist, sondern für eine tatsächliche Nichtexistenz eines exakten Energiewertes steht, stellen die oben angesprochenen Beispiele auch keine Verletzung des Energieprinzips dar, das nur dann angewendet werden kann, wenn die Energie einen definierten Wert annimmt. Mit dieser Einschränkung behält der Energiesatz auch in der Mikrophysik seine volle Gültigkeit.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.