Die zeitabhängige Schrödinger-Gleichung der Quantentheorie beschreibt eindeutig die Dynamik der Wellenfunktion, also deren zeitliche Entwicklung. Lösungen der Schrödinger-Gleichung verraten also den Zustand des Quantensystems zu einem Zeitpunkt t und an einem Ort r (Vektor).

von Schrödinger zu Wheeler-DeWitt

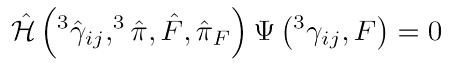Eine relativistische Formulierung der stationären Schrödinger-Gleichung kennt man als die Wheeler-DeWitt-Gleichung. Sie ist Gegenstand der Quantenkosmologie. Man erhält diese Gleichung, wenn man die Relativitätstheorie in Hamiltonsche Form umschreibt. Dieser Zugang ist bereits in der klassischen Mechanik bekannt, besitzt jedoch eine so allgemeine Formulierung, dass man ihn auch auf andere Theorien übertragen kann. Wichtig ist die Anmerkung, dass die Wheeler-DeWitt-Gleichung nicht kovariant ist. Das verwundert an sich nicht, wenn man berücksichtigt, dass die Schrödinger-Gleichung im Rahmen der nicht-relativistischen Quantenmechanik abgeleitet wird. Die Verletzung der Kovarianz manifestiert sich darin, dass bestimmte raumartige Hyperflächen ausgezeichnet sind. Außerdem gilt die Wheeler-DeWitt-Gleichung nur punktweise. Deshalb sind etwaige Renormierungsverfahren erforderlich.
Technisch muss man die Raum-Zeit-Symmetrie der Allgemeinen Relativitätstheorie wieder aufbrechen und in Raum und Zeit separieren. Diese als ADM-Formalismus (nach den Relativisten Arnowitt, Deser und Misner) bekannte Technik zeichnet raumartige Hyperflächen aus, deren Blätterung (Foliation) den Ablauf der Zeit darstellt: von einer Hyperfläche auf die andere ändert sich der kanonische Zeitparameter. Im üblichen Hamiltonschen Formalismus berechnet man nun die generalisierten kanonischen Impulse und die kanonisch konjugierte Variable aus den Ableitungen der Lagrange-Dichte. Integration liefert schließlich die Hamilton-Funktion. Sie ist der wesentliche Operator der Wheeler-DeWitt-Gleichung, die formal der (stationären) Schrödinger-Gleichung (zum Energieeigenwert null) sehr ähnelt. Die Wellenfunktion wird nun allerdings als die 'Wellenfunktion des Universums' bezeichnet. Sie ist auf einem unendlich-dimensionalen Superraum der Raumzeit-Geometrien und aller Materiefelder definiert.

So geht's weiter: Randbedingungen fixieren

An diese hyperbolische, partielle Differentialgleichung muss man nun Randbedingungen stellen, wie beispielsweise Vilenkin und Linde vorschlugen. Sie leiteten eine Analogie zum quantenmechanischen Tunneleffekt ab, das man 'Quantentunneln aus dem (bzw. in das) Nichts' nannte. Dies erklärte sich daraus, weil ein Wahrscheinlichkeitsstrom (mit der üblichen quantenmechanischen Definition) aus dem (bzw. in den) Superraum hinaus fließt.
Hartle und Hawking gaben eine alternative Randbedingung an, die 'no-boundary-condition'. Hier ist der Rand der vierdimensionalen Mannigfaltigkeit de facto immer derselbe. Das Problem dieses Zugangs über Pfadintegrale liegt darin, dass die Wellenfunktion des Universums dann nicht eindeutig festgelegt werden kann, weil eine Auswertung des Pfadintegrals in der komplexen Ebene zu verschiedenen Ergebnissen führt, je nachdem welchem Integrationsweg man folgt.

Erzeugung und Vernichtung ganzer Universen!

In der Quantenkosmologie gibt es auch den vertrauten Apparat der kanonischen Quantisierung. So kann man Vielteilchenzustände, Baby-Universen genannt, aus Vakuumzuständen, voids genannt, durch Anwendung von Erzeugungsoperatoren erzeugen. Allerdings wird die zugehörige Wheeler-DeWitt-Gleichung noch komplexer und sogar nicht-linear, weil Wechselwirkungen zwischen diesen Zuständen berücksichtigt werden müssen. Die quantenmechanische Teilchenerzeugung und -vernichtung entspricht in dieser Anwendung auf den Kosmos der Erzeugung und Vernichtung von Universen! Der erkenntnistheoretische Inhalt dieser Theorie ist immens.

Der zeitliche Aspekt

Die Wheeler-DeWitt-Gleichung ist in ihrer fundamentalen Formulierung unabhängig vom Parameter Zeit! Es gibt zwar einen Zeitparameter, der die Foliation der Raumzeit in Hyperflächen bestimmt. Die Foliation ist jedoch vollkommen willkürlich! Daher ist auch der resultierende Zeitbegriff nicht eindeutig. Es muss nun untersucht werden, ob die Quantentheorien verschiedener Foliationen ('Eichungen') unitär äquivalent sind. Träfe dies zu, wäre die gewählte Foliation irrelevant. Erst spezielle Lösungen der Wheeler-DeWitt-Gleichung (wenn man den lokalen Beobachter wieder einführen muss) leiten wieder auf einen Ordnungsparameter, den man mit der Zeit identifizieren kann. Dies führte in der Vergangenheit zu der Frage nach einer 'Physik ohne Zeit'.

Lesehinweis

• Web-Essay: Was ist Zeit?