Lexikon der Chemie: Atomspektroskopie
Atomspektroskopie, Teilgebiet der Spektroskopie, das die bei der Wechselwirkung elektromagnetischer Strahlung mit freien Atomen auftretenden Linienspektren untersucht. Da freie Atome Strahlung der gleichen Wellenlänge sowohl zu absorbieren wie zu emittieren vermögen, können Atomspektren als Emissions- und Absorptionsspektren oder auch als Kombination beider, als Fluoreszenzspektren (Atomfluoreszenzspektroskopie), beobachtet werden. Die einzelnen Linien, charakterisiert durch die Frequenz ν, der Spektren entsprechen gemäß der Gleichung
ΔE = E2 – E1 = h·ν (1)
der Energiedifferenz ΔE zwischen zwei definierten Energiezuständen E1,E2 des untersuchten Atoms; h ist das Plancksche Wirkungsquantum. In der hier behandelten optischen Atomspektroskopie, die sich auf die Betrachtung des optischen Teiles des Spektrums (UV, VIS, IR) beschränkt, entsprechen diese Energiezustände unterschiedlichen Anordnungen der Valenzelektronen. Elektronenübergänge innerer Elektronen führen zu Röntgenspektren (Röntgenspektroskopie). Damit die untersuchte Probe in Form freier Atome vorliegt, muß sie vorher entsprechend erhitzt werden.
Theoretische Grundlagen. Da die Spektren für die Atome, von denen sie absorbiert oder emittiert werden, spezifisch sind, müssen sie eng mit deren Bau und Eigenschaften zusammenhängen. Ihre Interpretation erfolgt deshalb mit Hilfe geeigneter Atommodelle (Bohr-Sommerfeldsches Atommodell, quantenmechanisches Atommodell). Eine Betrachtung verschiedener Atomspektren zeigt, daß die Anordnung der Spektrallinien von der Stellung des Elementes im Periodensystem abhängt. Elemente mit einem Valenzelektron, z. B. die Alkalimetalle, weisen linienarme Spektren, dagegen Elemente mit mehreren Valenzelektronen, z. B. die Nebengruppenelemente, sehr linienreiche Spektren auf. Das einfachste Atomspektrum ist das des neutralen Wasserstoffatoms. Es weist eine Reihe scharfer Linien auf, deren Abstand mit fallender Wellenlänge abnimmt (Abb. 1). Eine solche Linienfolge wird als Serie bezeichnet. Am kurzwelligen Ende drängen sich die Linien zu einer Häufungsstelle zusammen, die die Seriengrenze darstellt.

Atomspektroskopie. Abb. 1: Balmer-Serie des Wasserstoffspektrums.
Jenseits der Seriengrenze schließt sich das Seriengrenzkontinuum an, das durch den Übergang eines Elektrons aus einem diskreten Energiezustand in einen Zustand außerhalb des Atomverbandes oder umgekehrt entsteht. Die Zustände außerhalb des Atomverbandes sind nicht mehr gequantelt, so daß das Elektron beliebige kinetische Energien annehmen kann.
Im Spektrum des atomaren Wasserstoffs treten fünf derartige Serien auf. Die Wellenzahlen ν~ sämtlicher Linien des Wasserstoffspektrums können durch die Gleichung

(2)
dargestellt werden, wobei m die Hauptquantenzahl des höher angeregten Zustandes, n die Hauptquantenzahl des niedriger angeregten Zustandes oder des Grundzustandes des Wasserstoffatoms, R die Rydberg-Konstante (109677,759 cm-1) und Z die Kernladungszahl bedeuten. Die Wellenzahl einer Spektrallinie ergibt sich danach als Differenz zweier Ausdrücke Tn= R/n2 und Tm= R/m2, die man als Terme bezeichnet. Sie stellen die durch h·c dividierten Energiezustände der Atome dar (c ist die Lichtgeschwindigkeit). Eine Spektralserie entsteht, wenn zu einem festen Ausgangsterm R/n2 (Fixterm) ein Laufterm R/m2 durch Variation der Quantenzahl m eine Folge von Werten annimmt. Für die Serien des Wasserstoffs ergeben sich aus Gl. 2 unter Berücksichtigung von Z = 1 folgende Formeln:
Lyman-Serie (im UV)

m = 2, 3, 4, ... (3a)
Balmer-Serie (im Sichtbaren)

m = 3, 4, 5, ... (3b)
Paschen-Serie (im IR)

m = 4, 5, 6, ... (3c)
Bracket-Serie (im IR)
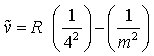
m = 5, 6, 7, ... (3d)
Pfund-Serie (im IR)
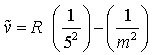
m = 6, 7, 8, ... (3e)
Es ist üblich, diese Zusammenhänge in Form eines Termschemas graphisch darzustellen, in dem die einzelnen Terme als horizontale Geraden eingetragen werden, so daß ihr Abstand unmittelbar die Wellenzahl der entsprechenden Spektrallinie angibt (Abb. 2). Es ist zu erkennen, wie die Terme gegen die Seriengrenze immer enger zusammenrücken.
Das H-Atom sollte grundsätzlich alle nach Abb. 2 möglichen Übergänge sowohl emittieren als auch absorbieren können. Da bei normaler Temperatur die H-Atome im Elektronengrundzustand (n= 1) vorliegen, ist eine Absorption aber nur für die Lyman-Serie möglich, deren unterster Term der Grundzustand ist. Die im Grundzustand endenden Linien werden als Resonanzlinien bezeichnet. Lediglich Resonanzlinien können in Emission und Absorption beobachtet werden. Alle anderen Serien treten nur in Emission auf, außer wenn die Atome bereits in einem angeregten Zustand vorliegen.
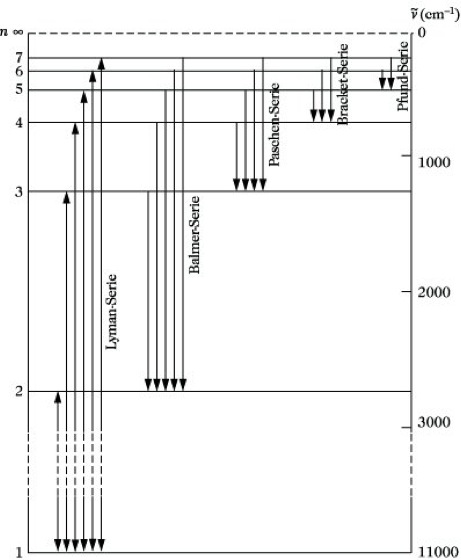
Atomspektroskopie. Abb. 2: Termschema des Wasserstoffatoms mit Spektralserien.
Dem Wasserstoffspektrum sehr ähnlich sind die Spektren des einfach positiv geladenen He+ und des doppelt positiv geladenen Li2+, die ebenfalls nur ein Elektron aufweisen. Entsprechend Gl. 2 liegen die Spektrallinien der Serien des He+ (Z = 2) bei viermal größeren Wellenzahlen als die des Wasserstoffs. Beim Li2+ (Z = 3) ist die Wellenzahl entsprechender Linien neunmal so groß wie beim Wasserstoff. Diese Gesetzmäßigkeiten sind Inhalt des spektroskopischen Verschiebungssatzes von Sommerfeld und Kossel, nach dem das Spektrum eines beliebigen Atoms stets dem des einfach positiv geladenen Ions des im Periodensystem ihm folgenden Elementes und dem des zweifach positiv geladenen Ions des übernächsten Elementes ähnelt. Relativ einfach sind die Spektren der Alkalimetalle, in denen das eine Valenzelektron ein "wasserstoffähnliches" Spektrum aufweist. Allerdings existiert eine größere Mannigfaltigkeit von Energiezuständen, die nicht mehr wie beim Wasserstoff durch eine einzige Quantenzahl, die Hauptquantenzahl, beschrieben werden können. Zur Kennzeichnung der Energieniveaus und der zwischen ihnen auftretenden Übergänge sind noch folgende 3 Quantenzahlen erforderlich:
- die Nebenquantenzahl oder Bahndrehimpulsquantenzahl l, die die Werte 0, 1 ... n – 1 annehmen kann, die man mit den Buchstaben s, p, d, f bezeichnet,
- die Spinquantenzahl s (auch ms), die die Werte +1/2 und -1/2 aufweist,
- die Gesamtdrehimpulsquantenzahl j, die sich durch vektorielle Addition von Bahndrehimpuls und Spin ergibt.
Das Auftreten verschiedener Termserien (Abb. 3) wird als Folge verschiedener Werte des Bahndrehimpulses (s, p, d, f) gedeutet. Die beobachteten Serien lassen sich folgendermaßen charakterisieren: Hauptserie s – np, scharfe Nebenserie p – ns, diffuse Nebenserie p – nd, Fundamental- (Bergmann-) Serie d – nf.

Atomspektroskopie. Abb. 3.: Vereinfachtes Termschema des Natriumatoms mit den den verschiedenen Spektralserien entsprechenden Übergängen.
In der Hauptserie erfolgen Elektronenübergänge aus p-Zuständen unterschiedlicher Hauptquantenzahl n in den niedrigsten s-Zustand (Grundzustand), in der ersten Nebenserie von s-Zuständen in den niedrigsten p-Zustand usw. Im Gegensatz zum Wasserstoffatom kommen nicht mehr alle möglichen Übergänge zwischen den vorhandenen Energiezuständen tatsächlich vor, sondern nur solche, für die die Auswahlregel Δl = ±1 erfüllt ist. Eine nähere Betrachtung der Alkalispektren zeigt weiter, daß alle Linien als Doppellinien auftreten. Dies ist mit Hilfe der Gesamtdrehimpulsquantenzahl j erklärbar. Für l = 1 ergeben sich infolge der beiden Einstellmöglichkeiten s = ±1/2 die beiden Quantenzahlen j= +1/2 und j = -1/2 für l = 0 wegen der nur einfachen Einstellmöglichkeit von s der Wert j = 1/2. Als Folge davon sind alle Terme mit Ausnahme der s-Zustände Dubletterme, wobei die Größe der Dublettaufspaltung mit wachsender Ordnungszahl des Alkalimetalls stark zunimmt. Es sind nur Übergänge für Δj = 0, ±1 erlaubt. Diese auf der gequantelten Wechselwirkung von Bahndrehimpuls und Spin beruhende Aufspaltung der Spektrallinien in Multipletts wird als Feinstruktur der Spektrallinien bezeichnet.
Bei Systemen mit mehreren Valenzelektronen nimmt die Kompliziertheit der Spektren weiter zu. Die Drehimpulse l und s der einzelnen Elektronen addieren sich vektoriell zu den Gesamtimpulsen L und S:l1, l2, l3 ... L und s1, s2, s3 ... S. Diese setzen sich nach der Russel-Saunders-Kopplung zur Gesamtdrehimpulsquantenzahl J zusammen.
Zur Kennzeichnung der einzelnen Terme wird eine bestimmte Symbolik verwendet. So bedeutet 3 2P3/2 einen Zustand mit der Hauptquantenzahl 3 und L= 1 (P). Die links oben angegebene Zahl 2 weist die Multiplizität des Terms (2 S + 1), der rechts tiefgestellte Ausdruck 3/2 den Wert von J aus.
Atomspektroskopie. Tab. 1: Spektroskopischer Wechselsatz.
| ||||||||
| Multiplizität | 2 | 1,3 | 2,4 | 1,3,5 | 2,4 | 1,3 | 2 |
Atomspektroskopie. Tab. 2: Atomspektroskopische Analysenverfahren.
| ||||||
| Fest oder Lösung | Bogen, Funken induktiv gekoppeltes Plasma | elektrisch (Wärme) | Emission | Atomemissionsspektroskopie und -spektrographie, AES | qualitative und quantitative Analyse | |
| Lösung | Flamme | elektrisch (Wärme) | Emission | Flammenspektralphotometrie | quantitative Analyse | |
| Lösung | Flamme | chemisch u. spez. Lichtquellen | Absorption | Atomabsorptionsspektrometrie, AAS, Flammen-AAS | quantitative Analyse | |
| Lösung | Flamme | chemisch (Wärme) spez. Lichtquellen | Fluoreszenz | Atomfluoreszenzspektrometrie, AFS, Flammen-AFS | quantitative Analyse | |
| Lösung Mikromenge | Graphitrohr- küvette | elektrische Widerstandserhitzung | Emission | Graphitrohr-AES | quantitative Analyse | |
| Lösung Mikromenge | Graphitrohr- küvette | elektrische Widerstandserhitzung | Absorption | Graphitrohr-AAS | quantitative Analyse | |
| Lösung Mikromenge | Graphitrohrküvette spezieller Bauart | elektrische Widerstandserhitzung | Fluoreszenz | flammenlose AFS | quantitative Analyse |
In den Spektren von Atomen mit mehr als einem Valenzelektron, z. B. den Erdalkalimetallen, kommen mehrere, im allg. nicht miteinander kombinierende Termsysteme vor, die sich in ihrer Multiplizität unterscheiden. Bei den Erdalkalimetallen mit 2 Valenzelektronen ist dies ein Singulett- und ein Triplettsystem. Jedes dieser Systeme besteht aus einer Reihe von Serien ähnlich den Alkalimetallen. Eine weitere Komplizierung wird durch die Möglichkeit der gleichzeitigen Anregung beider Valenzelektronen (Doppelanregung) bewirkt. Allgemein wechseln beim Fortschreiten im Periodensystem gerade und ungerade Multiplizitäten ab (Tab. 1). Zu geraden Elektronenzahlen gehören ungerade Multiplizitäten und umgekehrt (spektroskopischer Wechselsatz). Die genannten und noch einige andere Fakten führen dazu, daß insbesondere bei Elementen höherer Ordnungszahl der Seriencharakter nur noch schwer erkennbar ist und die Spektren unübersichtlich erscheinen.
Bei hoher Auflösung zeigt sich außer der Feinstruktur eine weitere Aufspaltung, die Hyperfeinstruktur. Diese meist äußerst geringe Aufspaltung von Spektrallinien erfolgt durch Wechselwirkung von Elektronen mit dem Atomkern. Sie kann einmal dadurch bedingt sein, daß das betreffende Element aus mehreren Isotopen besteht, oder auf einer Wechselwirkung mit dem Kernspin beruhen. Die Aufspaltung von Spektrallinien in einem äußeren elektrischen Feld wird als Stark-Effekt, die in einem äußeren magnetischen Feld als Zeeman-Effekt bezeichnet.
Anwendung. Atomspektroskopische Analysenverfahren können zur qualitativen und quantitativen Stoffanalyse eingesetzt werden. Wird ein Atom durch Energiezufuhr in einen angeregten Zustand überführt, so kann es die Anregungsenergie durch Emission eines Photons wieder abgeben. Dieser Prozeß bildet die Grundlage der Atomemissionsspektrometrie und Flammenspektralphotometrie. Die Absorption von Photonen ist die Grundlage der Atomabsorptionsspektrometrie. Wird die durch Absorption von Photonen aufgenommene Energie ganz oder teilweise wieder in Form eines Photons abgegeben, so liegt Atomfluoreszenz vor. Die auf den geschilderten Lichtemissions- und -absorptionsprozessen beruhenden atomspektroskopischen Analysenverfahren sind in Tab. 2 zusammengestellt.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.