Das ist eines der wesentlichen Prinzipien, das Albert Einstein zu seiner Allgemeinen Relativitätstheorie (ART) inspirierte. Daneben sind das Äquivalenzprinzip, das Kovarianzprinzip, das Korrespondenzprinzip und das Machsche Prinzip zu nennen.

Warum schwer machen, wenn's einfach geht?

Das Prinzip minimaler, gravitativer Kopplung dürfte dasjenige unter den fünf sein, das am wenigsten bekannt ist. Letztendlich ist es ein Leitprinzip, das in allgemeiner Form fast alle Physiker und Mathematiker verfolgen: ein Prinzip der Einfachheit. Die meisten physikalischen (aber auch andere wissenschaftliche) Modelle sind dadurch geprägt, das zunächst der simpelste Zugang zu einer Problemstellung gewählt wird. Das gilt besonders dann, wenn es sich um die 'ersten Schritte' auf wissenschaftlichem Neuland handelt. Es geht darum, ein prinzipielles Verhalten eines Systems unter einfachsten Bedingungen zu erforschen. Erst danach wird das Modell komplexer, kompliziertere Wechselwirkungen werden miteinbezogen oder höhere Ordnungen werden betrachtet. Im Kern ist es wohl gerade das, was man mit analytischem Denken in der Naturwissenschaft meint. Eine naturwissenschaftliches Problem wird analysiert, also in Bestandteile zerlegt. Die Komponenten werden in einem logischen Zusammenhang zueinander gebracht und deren Wechselwirkung erörtert. In der Regel beschreibt eine mathematische Gleichung oder ein System gekoppelter Gleichungen (häufig Differentialgleichungen) die Dynamik des Systems. Diese Gleichungen werden mit wohl bekannten (in der Regel numerischen, nicht analytischen) Techniken gelöst. D.h. das Problem ist in dem Sinne gelöst, dass der Naturwissenschaftler ein Verhalten in Vergangenheit oder Zukunft vorhersagen kann bzw. ein in der Natur beobachtetes Phänomen erklären kann. Erklären heißt wiederum, dass er die komplexe, wechselseitige Beeinflussung der Systemteile logisch und plausibel verknüpfen kann.

Was bringt's Einstein?

Der simplifizierende Ansatz in der Modellbildung lässt auf die Relativitätstheorie folgendermaßen anwenden: angenommen die Gleichungen der Speziellen Relativitätstheorie (SRT) seien bereits bekannt. So folgen die Gleichungen der ART – die dann erst eine Gravitationstheorie darstellt – unter anderem dann, wenn unnötig komplizierte Terme beim Übergang von SRT nach ART weggelassen werden. Diese vage Formulierung wird konkret, wenn also beispielsweise partielle Ableitungen lediglich in kovariante Ableitungen verwandelt werden, ohne zusätzliche Terme, die beispielsweise den Krümmungstensor enthalten. Minimale gravitative Kopplung ist so zu verstehen, dass so wenig neue Terme mit dem Krümmungstensor wie möglich auftreten, wenn man den Übergang von SRT nach ART vollzieht.

Beispiel: der Einstein-Tensor

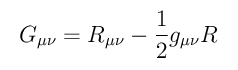Der Einstein-Tensor G_μν stellt gerade die linke Seite der Einsteinschen Feldgleichungen dar. Es ist die 'geometrische Seite', die den Riemannschen Krümmungstensor in verschiedenen Verjüngungen (als Ricci-Tensor und Ricci-Skalar) enthält. Er ist rechts als Gleichung dargestellt. Aber wie kommt man gerade darauf, dass der Einstein-Tensor so aussehen muss? Das ist nicht-trivial! Der Tensor wurde nicht umsonst nach Einstein benannt: Es hat ihn und seinen Freund Marcel Grossmann mehrere Jahre gekostet, um diese Gestalt abzuleiten! Das Prinzip minimaler gravitativer Kopplung hat bei der Bestimmung dieser Gleichung sicher eine Rolle gespielt, denn es sind auch kompliziertere Enstein-Tensoren denkbar.