Gitterenergie, die Energie, die beim Zusammentritt der isolierten Kristallbausteine zu einem Kristallgitter frei wird. Sie wird meist auf ein Mol der betreffenden Kristallsubstanz bezogen und dann als molare G. E_G bezeichnet. Da die G. nach der gegebenen Definition einem exothermen Vorgang zugeordnet ist, werden ihre Werte nach der üblichen Vorzeichenkonvention in der Thermodynamik mit einem negativen Vorzeichen versehen. Häufig wird die G. aber auch mit dem umgekehrten Vorgang, der isothermen Überführung des Kristalles in das ideale Gas seiner Bausteine, in Beziehung gebracht und dann als endotherme Größe mit positivem Vorzeichen ihrer Werte behandelt.

Die G. ist ein Maß für die Stabilität einer Kristallstruktur. Sie steht deshalb in engem, gesetzmäßigem Zusammenhang mit anderen Kristalleigenschaften, z. B. Schmelztemperatur, Kompressibilität, thermische Ausdehnung, Härte und anderen mechanischen Eigenschaften. Beim Vorliegen von Polymorphie ist die Modifikation mit dem größten Betrag an G. meist auch die thermodynamisch stabilste. Es muß aber beachtet werden, daß für die Stabilität eines Zustandes die freie Energie entscheidend ist und bei deren Berechnung neben der inneren Energie auch noch die Entropie berücksichtigt werden muß, für die Entropieberechnungen von Gittern unterschiedlicher Symmetrie aber noch keine zuverlässigen Ansätze vorliegen.

Eine direkte experimentelle Bestimmung der G. gelingt nur in den Fällen, in denen der Übergang zwischen den beiden Bezugszuständen Kristall und aus den freien Kristallbausteinen bestehendes Gas eindeutig ist und die mit ihm verbundene Energie gemessen werden kann. Die Möglichkeiten dafür sind bei den einzelnen Gittertypen recht unterschiedlich und durch die Bildung von Ionenpaaren, Atomclustern, Molekülassoziaten und anderen höheraggregierten Gaspartikeln stark eingeschränkt. Man kann die G. aber häufig indirekt aus thermochemischen und spektroskopischen Daten experimentell ermitteln (Born-Haber-Kreisprozeß). Zur theoretischen Berechnung der G. benutzt man geeignete Ansätze für die Wechselwirkungspotentiale zwischen den Kristallbausteinen. Für Ionengitter sind dabei neben der Coulomb-Wechselwirkung auch noch die Abstoßungskräfte zu berücksichtigen, die bei starker Annäherung der Ionen auftreten (chemische Bindung). Nach Born ergibt sich bei einem kürzesten Abstand R und den Ladungszahlen z₊ und z_- ungleich geladener Ionen für die G.

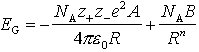
Hierbei sind N_A Avogadro-Konstante, e Elementarladung, A die für den jeweiligen Gittertyp charakteristische Madelung-Konstante, ε₀ elektrische Feldkonstante, n Bornscher Abstoßungsexponent (n >> 1, je nach Ionenpaar zwischen 6 und 12), B Stoffkonstante. Für den Gleichgewichtsabstand R₀ im Kristall liegt ein Minimum der potentiellen Energie vor; aus der entsprechenden Bedingung dE_G/dR = 0 folgt

Die mit Hilfe dieser Gleichung berechneten Werte für die G. stehen für typische Ionensubstanzen, wie z. B. die Alkalihalogenide, in guter Übereinstimmung mit den experimentellen Ergebnissen. Größere Differenzen, etwa ab 5 %, weisen auf beträchtliche kovalente Bindungsanteile und stärkere Abweichungen von der kugelsymmetrischen Ladungsverteilung der Ionen infolge Polarisation hin, sie sind für die Diskussion der Bindungskräfte im Kristall von Interesse. Wie aus der Gleichung hervorgeht, sind die entscheidenden Faktoren für die G. von Ionenkristallen die Gittersymmetrie, die Abstände und vor allem die Ladungszahlen der Ionen. So beträgt z. B. die G. für Natriumchlorid NaCl -765 kJ mol^-1, für Natriumbromid NaBr -731 kJ mol^-1, für Magnesiumoxid MgO -3925 kJ mol^-1 und für Thoriumoxid ThO₂ -20100 kJ mol^-1.

Für Metallgitter kann man die G. auf der Grundlage des Elektronengasmodells als diejenige Energie definieren, die beim Zusammentritt der gasförmigen Kationen und Elektronen zum Metallkristall frei wird. Sie läßt sich einmal als Summe von Sublimations- und Ionisierungsenergie experimentell bestimmen und zum anderen nach einer Beziehung berechnen, die der für die Berechnung der G. von Ionenkristallen analog ist. Trotz der starken Vereinfachung dieser Modellbetrachtung erhält man vor allem für die Alkalimetalle eine überraschend gute Übereinstimmung zwischen theoretischen und experimentellen Werten. Die G. beträgt z. B. für Natrium -604 kJ mol^-1 und für Kupfer -1087 kJ mol^-1.

Bei der Berechnung der G. für Van-der-Waals-Gitter, wie sie Molekülkristallen zugrunde liegen, sind alle Möglichkeiten des Auftretens verschiedenartiger zwischenmolekularer Wechselwirkungskräfte zu berücksichtigen. Die G. von Van-der-Waals-Gittern liegen etwa bei 3 bis 15 kJ mol^-1 (Edelgase) bzw. 40 bis 80 kJ mol^-1 (organische Molekülsubstanzen).