Der Maxwell-Tensor ist ein Tensor und damit ein Objekt von Einsteins Relativitätstheorie. Dieser Tensor heißt auch elektromagnetischer Feldstärketensor und ist eingebettet in eine kovariante Formulierung der Elektrodynamik, d.h. die klassische Maxwellsche Theorie wurde relativistisch verallgemeinert.

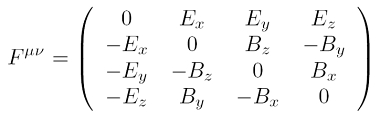
Wie sieht so ein Tensor aus?

Der Maxwell-Tensor wurde oben als Matrix dargestellt. Wie man sieht enthält er sowohl Komponenten des elektrischen Feldes (E), als auch des Magnetfeldes (B). Die Indizes x,y,z stehen dabei für die drei Raumrichtungen in kartesischen Koordinaten. Die Kenner der Matrizen sehen auch, dass der Maxwell-Tensor offensichtlich nicht symmetrisch ist: spiegelt man die Komponenten des Tensors an der Hauptdiagonalen, so erhält man zwar die gleiche Komponente des Feldes, aber umgekehrtes Vorzeichen. In Einsteins Theorie schreibt man das kompakt so: F_μν = – F_νμ.

Aus 4 mach 2

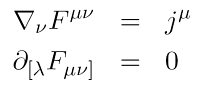Der Maxwell-Tensor bündelt also in kompakter Schreibweise die Komponenten des elektrischen und magnetischen Feldes. Damit ermöglicht er eine sehr elegante und kompakte kovariante Schreibweise der vier Maxwellschen Gleichungen der klassischen Elektrodynamik. Im Vakuum und in einer flachen Raumzeit, also für die Minkowski-Geometrie der Speziellen Relativitätstheorie (SRT) reduzieren sich die Maxwellschen Gleichungen auf zwei Gleichungen, wie in der Abbildung links dargestellt.

Elektrodynamik in gekrümmten Raumzeiten

In der Allgemeinen Relativitätstheorie konstituiert dieser Tensor zusammen mit dem metrischen Tensor den Energie-Impuls-Tensor des elektromagnetischen Tensors. Damit wird eine Behandlung der Elektrodynamik in gekrümmten Raumzeiten möglich. Es resultieren dann die so genannten Einstein-Maxwell-Gleichungen. Als Lösungen dieser Nicht-Vakuum-Feldgleichungen kennt man eine statische, elektrische Punktladung, die Reissner-Nordstrøm-Lösung, und eine rotierende, elektrische Ringladung, die so genannte Kerr-Newman-Lösung. Letztere repräsentiert eine sehr allgemeine Form von Schwarzes Löchern 'mit den meisten Haaren' (vergleiche Keine-Haare-Theorem). Es weist die physikalischen Eigenschaften Masse, Drehimpuls und elektrische Ladung auf.

relativistische Astrophysik: SRMHD & GRMHD

Der Maxwell-Tensor wird ebenfalls benötigt, wenn die Astrophysiker Plasmen beschreiben wollen und dabei relativistische Effekte voll berücksichtigen wollen. In der flachen Raumzeit der SRT heißt dieses Forschungsfeld Speziell Relativistische Magnetohydrodynamik, (special relativistic magnetohydrodynamics, SRMHD). Forschungsgegenstand sind dann z.B. die fast lichtschnellen Jets von radiolauten Quasaren und Radiogalaxien (also von Aktiven Galaktischen Kernen). Diese extrem schnellen Materieströmungen werden mit aufwendigen Berechnungen auf Supercomputern simuliert.
Geht man zu den gekrümmten Raumzeiten über, so sprechen die Astrophysiker von Allgemein Relativistischer Magnetohydrodynamik, (general relativistic magnetohydrodynamics, GRMHD). Forschungsgegenstand ist dann beispielsweise die unmittelbare Umgebung eines Schwarzen Loches, wo die Wechselwirkung des Loches mit (als Flüssigkeit beschriebene) Materie und Akkretion untersucht werden.