Der Weyl-Tensor oder auch konforme Tensor genannt wurde benannt nach dem deutschen Mathematiker Hermann Klaus Hugo Weyl (1885 – 1955). Dieser Tensor 4. Stufe ist relativ kompliziert und kann zunächst für beliebige Dimensionen n allgemein notiert werden. In der Allgemeinen Relativitätstheorie (ART) gilt n = 4, weil Raumzeiten durch eine Zeitdimension und drei Raumdimensionen charakterisiert sind.

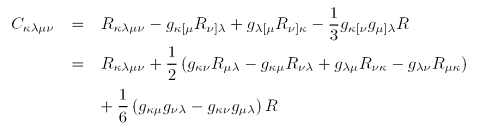
Berechnung des Weyl-Tensors

Anhand der Definitionsgleichung oben sieht man unmittelbar, dass der Weyl-Tensor ein recht kompliziertes Gebilde ist, das schon bei einfachen Raumzeiten nur mit einigem Aufwand zu berechnen ist. Es sei denn man nutzt so genannte computer-algebraische Systeme, die Tensorrechnungen am Computer bequem und schnell erlauben.
Die Gleichung zeigt auch, dass sich der Weyl-Tensor aus dem Riemann-Tensor (Krümmungstensor; R mit vier Indizes), dem Ricci-Tensor (R mit zwei Indizes) und dem Ricci-Skalar (R ohne Indizes) berechnen lässt.

Symmetrien

Neben den Symmetrien des Riemann-Tensors besitzt der Weyl-Tensor eine zusätzliche Symmetrie: er ist spurfrei, das heißt die Summe seiner Diagonalelemente verschwindet. Die Diskussion seiner Symmetrieeigenschaften lässt eine Klassifikation der Vakuum-Raumzeiten zu, die unter der Petrov-Klassifikation bekannt ist.

Indikator der Krümmungseigenschaften

Physikalisch ist der Weyl-Tensor besonders von Bedeutung, weil er sich zur Untersuchung der Krümmungseigenschaften von Raumzeiten eignet. Aus Riemann-Tensor und Weyl-Tensor lassen sich Riemannsche und Weylsche Invarianten bestimmen, die nicht vom Koordinatensystem abhängen. Dazu gehört auch der Kretschmann-Skalar. Eine Diskussion solcher Größen macht klar, wo die Krümmung besonders stark oder besonders schwach ist. Das erleichtert das Auffinden von Krümmungssingularitäten und die Charakterisierung als asymptotisch flache Raumzeit.