Start
Web-Artikel
Lexikon
Vorträge
Ausbildung
Essays
Rhetorik
Links
Autor
Kontakt



Astro-Lexikon W 2
Die Wellenfunktion, üblicherweise symbolisiert durch den griechischen Buchstaben Ψ, beschreibt in der Quantentheorie ein mikroskopisches Teilchen.
Von der klassischen Mechanik zur Quantenmechanik
In der klassischen Mechanik bestimmt man Teilchenbahnen, indem man das Bewegungsproblem, nämlich die
Bewegungsgleichung, löst. Das Resultat ist eine Teilchenbahn, die von bestimmten Einstellparametern
abhängen mag, aber wohl definiert und diskret ist.
In der Quantenmechanik löst nun die Wellenfunktion das Konzept der Teilchenbahn ab (sie muss aber noch geeignet
interpretiert werden, dazu später) und löst ebenfalls eine quantenmechanische Bewegungsgleichung: die berühmte
Schrödinger-Gleichung. Wie wir sehen werden ist dann die Bahn des quantenmechanischen Teilchens, des
Quants, nicht mehr so gut bestimmt.
Eigenschaften der Wellenfunktion
Da die Wellenfunktionen quantenmechanische Teilchen beschreiben, müssen sie auch alle Eigenschaften von Teilchen enthalten können. Die Quantenphysiker nennen diese Eigenschaften Quantenzahlen und meinen damit z.B. die Masse des Teilchens, die elektrische Ladung, den Spin und den Isospin. Weiterhin hängt die Wellenfunktion von den Raumkoordinaten und der Zeit ab.
Wahrscheinlichkeitswelle
 Die Wellenfunktion ist eine skalare Verteilungsfunktion bestimmter Amplitude (Wellenamplitude), die im Allgemeinen vom
Ort und der Zeit abhängt und außerdem durch die Teilcheneigenschaften parametrisiert ist. Ein quantenmechanisches
Problem gilt als gelöst, wenn der charakteristische Verlauf der Wellenfunktion in den Koordinaten bekannt ist.
Das klassische Punktteilchen ist nicht mehr an einem bestimmten Punkt in Raum und Zeit lokalisiert, sondern in Form der Wellenfunktion
'verschmiert'. Dabei ist nicht die Wellenfunktion selbst von Bedeutung, sondern ihr Absolutquadrat. Denn die Wellenfunktion kann
auch komplexwertig sein. Absolutquadrate sind reellwertig. Anmerkung: Ein Absolutquadrat berechnet man immer dadurch, dass man eine gegebene
komplexe Größe mit der zugehörigen komplex konjugierten Größe (symbolisiert mit einem zusätzlichen Stern,
siehe Gleichung oben) multipliziert. Diese Verteilung des Absolutquadrats (nicht der Wellenfunktion selbst!) wird als
Wahrscheinlichkeitsverteilung interpretiert. Eine höhere Wahrscheinlichkeit das Quant anzutreffen wird dort erwartet, wo das
Absolutquadrat größer ist.
Die Wellenfunktion ist eine skalare Verteilungsfunktion bestimmter Amplitude (Wellenamplitude), die im Allgemeinen vom
Ort und der Zeit abhängt und außerdem durch die Teilcheneigenschaften parametrisiert ist. Ein quantenmechanisches
Problem gilt als gelöst, wenn der charakteristische Verlauf der Wellenfunktion in den Koordinaten bekannt ist.
Das klassische Punktteilchen ist nicht mehr an einem bestimmten Punkt in Raum und Zeit lokalisiert, sondern in Form der Wellenfunktion
'verschmiert'. Dabei ist nicht die Wellenfunktion selbst von Bedeutung, sondern ihr Absolutquadrat. Denn die Wellenfunktion kann
auch komplexwertig sein. Absolutquadrate sind reellwertig. Anmerkung: Ein Absolutquadrat berechnet man immer dadurch, dass man eine gegebene
komplexe Größe mit der zugehörigen komplex konjugierten Größe (symbolisiert mit einem zusätzlichen Stern,
siehe Gleichung oben) multipliziert. Diese Verteilung des Absolutquadrats (nicht der Wellenfunktion selbst!) wird als
Wahrscheinlichkeitsverteilung interpretiert. Eine höhere Wahrscheinlichkeit das Quant anzutreffen wird dort erwartet, wo das
Absolutquadrat größer ist.
Welle-Teilchen-Dualismus
In der Quantenphysik können sich Teilchen als Welle oder als Teilchen verhalten, d.h. in dem einen Experiment eignen sich die Welleneigenschaften zur Klärung der Beobachtung; in einem anderen eignen sich die Teilchen- oder Korpuskulareigenschaften. Dieses Phänomen heißt Welle-Teilchen-Dualismus und ist charakteristisch für Quanten. Dieser Dualismus gilt somit beispielsweise für Licht, genauer gesagt für Photonen, aber auch für Elektronen, für das Neutrino oder für den Atomkern.
Mikrowelt ist prinzipiell verschwommen
Hinzu kommt eine weitere Komplikation in der Quantenwelt: Es ist für quantenmechanische Beobachter nicht möglich, gewisse Eigenschaften eine Quants gleichzeitig zu messen: Ein Quantenbeobachter kann entweder den Ort oder den Impuls (die Geschwindigkeit) eines Quants messen. Ein Quantenbeobachter kann aber auch nur entweder die Energie oder die Zeit messen. Diese Unschärfen werden in der Heisenbergschen Unschärferelation zusammengefasst.
Zum quantenmechanischen Messprozess
Was mit der Wellenfunktion beim quantenmechanischen Messprozess geschieht, wird im Eintrag Kopenhagener Deutung erläutert. Die Interpretation birgt grundlegende Konsequenzen für unser Weltverständnis.
Dieses Postulat wurde 1923 von H. Weyl entworfen und besagt, dass sich die Galaxien im Universum wie 'Elementarteilchen' in einer Flüssigkeit bewegen sollen. Ein den Raum durchdringendes Substrat kann in diesem Sinne als eine ideale Flüssigkeit angesehen werden, weil sich die Geodäten nur einem singulären Punkt in der Vergangenheit (und evt. auch Zukunft) schneiden. Die Materie (Galaxien) besitzt daher in jedem Punkt der Raumzeit eine eindeutige Geschwindigkeit.
Der Weyl-Tensor oder auch konforme Tensor genannt wurde benannt nach dem deutschen Mathematiker Hermann Klaus Hugo Weyl (1885 - 1955). Dieser Tensor 4. Stufe ist relativ kompliziert und kann zunächst für beliebige Dimensionen n allgemein notiert werden. In der Allgemeinen Relativitätstheorie (ART) gilt n = 4, weil Raumzeiten durch eine Zeitdimension und drei Raumdimensionen charakterisiert sind.

Berechnung des Weyl-Tensors
Anhand der Definitionsgleichung oben sieht man unmittelbar, dass der Weyl-Tensor ein recht kompliziertes Gebilde ist, das schon
bei einfachen Raumzeiten nur mit einigem Aufwand zu berechnen ist. Es sei denn man nutzt so genannte computer-algebraische Systeme,
die Tensorrechnungen am Computer bequem und schnell erlauben.
Die Gleichung zeigt auch, dass sich der Weyl-Tensor aus dem Riemann-Tensor (Krümmungstensor;
R mit vier Indizes), dem Ricci-Tensor (R mit zwei Indizes) und dem
Ricci-Skalar (R ohne Indizes) berechnen lässt.
Symmetrien
Neben den Symmetrien des Riemann-Tensors besitzt der Weyl-Tensor eine zusätzliche Symmetrie: er ist spurfrei, das heißt die Summe seiner Diagonalelemente verschwindet. Die Diskussion seiner Symmetrieeigenschaften lässt eine Klassifikation der Vakuum-Raumzeiten zu, die unter der Petrov-Klassifikation bekannt ist.
Indikator der Krümmungseigenschaften
Physikalisch ist der Weyl-Tensor besonders von Bedeutung, weil er sich zur Untersuchung der Krümmungseigenschaften von Raumzeiten eignet. Aus Riemann-Tensor und Weyl-Tensor lassen sich Riemannsche und Weylsche Invarianten bestimmen, die nicht vom Koordinatensystem abhängen. Dazu gehört auch der Kretschmann-Skalar. Eine Diskussion solcher Größen macht klar, wo die Krümmung besonders stark oder besonders schwach ist. Das erleichtert das Auffinden von Krümmungssingularitäten und die Charakterisierung als asymptotisch flache Raumzeit.
Die zeitabhängige Schrödinger-Gleichung der Quantentheorie beschreibt eindeutig die Dynamik der Wellenfunktion, also deren zeitliche Entwicklung. Lösungen der Schrödinger-Gleichung verraten also den Zustand des Quantensystems zu einem Zeitpunkt t und an einem Ort r (Vektor).
von Schrödinger zu Wheeler-DeWitt
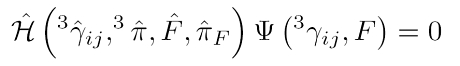 Eine relativistische Formulierung der stationären Schrödinger-Gleichung
kennt man als die Wheeler-DeWitt-Gleichung. Sie ist Gegenstand der Quantenkosmologie. Man
erhält diese Gleichung, wenn man die Relativitätstheorie in Hamiltonsche Form umschreibt.
Dieser Zugang ist bereits in der klassischen Mechanik bekannt, besitzt jedoch eine so allgemeine Formulierung, dass man ihn auch auf
andere Theorien übertragen kann. Wichtig ist die Anmerkung, dass die Wheeler-DeWitt-Gleichung nicht
kovariant ist. Das verwundert an sich nicht, wenn man berücksichtigt, dass die Schrödinger-Gleichung
im Rahmen der nicht-relativistischen Quantenmechanik abgeleitet wird. Die Verletzung der Kovarianz
manifestiert sich darin, dass bestimmte raumartige Hyperflächen ausgezeichnet sind. Außerdem gilt die Wheeler-DeWitt-Gleichung nur
punktweise. Deshalb sind etwaige Renormierungsverfahren erforderlich.
Eine relativistische Formulierung der stationären Schrödinger-Gleichung
kennt man als die Wheeler-DeWitt-Gleichung. Sie ist Gegenstand der Quantenkosmologie. Man
erhält diese Gleichung, wenn man die Relativitätstheorie in Hamiltonsche Form umschreibt.
Dieser Zugang ist bereits in der klassischen Mechanik bekannt, besitzt jedoch eine so allgemeine Formulierung, dass man ihn auch auf
andere Theorien übertragen kann. Wichtig ist die Anmerkung, dass die Wheeler-DeWitt-Gleichung nicht
kovariant ist. Das verwundert an sich nicht, wenn man berücksichtigt, dass die Schrödinger-Gleichung
im Rahmen der nicht-relativistischen Quantenmechanik abgeleitet wird. Die Verletzung der Kovarianz
manifestiert sich darin, dass bestimmte raumartige Hyperflächen ausgezeichnet sind. Außerdem gilt die Wheeler-DeWitt-Gleichung nur
punktweise. Deshalb sind etwaige Renormierungsverfahren erforderlich.
Technisch muss man die Raum-Zeit-Symmetrie der Allgemeinen Relativitätstheorie wieder aufbrechen und
in Raum und Zeit separieren. Diese als ADM-Formalismus (nach den Relativisten
Arnowitt, Deser und Misner) bekannte Technik zeichnet raumartige Hyperflächen aus, deren Blätterung (Foliation) den
Ablauf der Zeit darstellt: von einer Hyperfläche auf die andere ändert sich der kanonische Zeitparameter. Im üblichen Hamiltonschen Formalismus
berechnet man nun die generalisierten kanonischen Impulse und die kanonisch konjugierte Variable aus den Ableitungen der Lagrange-Dichte. Integration
liefert schließlich die Hamilton-Funktion. Sie ist der wesentliche Operator der Wheeler-DeWitt-Gleichung, die formal der (stationären)
Schrödinger-Gleichung (zum Energieeigenwert null) sehr ähnelt. Die Wellenfunktion wird nun allerdings als die 'Wellenfunktion des
Universums' bezeichnet. Sie ist auf einem unendlich-dimensionalen Superraum der
Raumzeit-Geometrien und aller Materiefelder definiert.
So geht's weiter: Randbedingungen fixieren
An diese hyperbolische, partielle Differentialgleichung muss man nun Randbedingungen stellen, wie beispielsweise Vilenkin und
Linde vorschlugen. Sie leiteten eine Analogie zum quantenmechanischen Tunneleffekt ab, das
man 'Quantentunneln aus dem (bzw. in das) Nichts' nannte. Dies erklärte sich daraus, weil ein Wahrscheinlichkeitsstrom
(mit der üblichen quantenmechanischen Definition) aus dem (bzw. in den) Superraum hinaus fließt.
Hartle und Hawking gaben eine alternative Randbedingung an, die 'no-boundary-condition'. Hier ist der Rand der
vierdimensionalen Mannigfaltigkeit de facto immer derselbe. Das Problem dieses Zugangs über Pfadintegrale liegt darin, dass die
Wellenfunktion des Universums dann nicht eindeutig festgelegt werden kann, weil eine Auswertung des Pfadintegrals in der
komplexen Ebene zu verschiedenen Ergebnissen führt, je nachdem welchem Integrationsweg man folgt.
Erzeugung und Vernichtung ganzer Universen!
In der Quantenkosmologie gibt es auch den vertrauten Apparat der kanonischen Quantisierung. So kann man Vielteilchenzustände, Baby-Universen genannt, aus Vakuumzuständen, voids genannt, durch Anwendung von Erzeugungsoperatoren erzeugen. Allerdings wird die zugehörige Wheeler-DeWitt-Gleichung noch komplexer und sogar nicht-linear, weil Wechselwirkungen zwischen diesen Zuständen berücksichtigt werden müssen. Die quantenmechanische Teilchenerzeugung und -vernichtung entspricht in dieser Anwendung auf den Kosmos der Erzeugung und Vernichtung von Universen! Der erkenntnistheoretische Inhalt dieser Theorie ist immens.
Der zeitliche Aspekt
Die Wheeler-DeWitt-Gleichung ist in ihrer fundamentalen Formulierung unabhängig vom Parameter Zeit! Es gibt zwar einen Zeitparameter, der die Foliation der Raumzeit in Hyperflächen bestimmt. Die Foliation ist jedoch vollkommen willkürlich! Daher ist auch der resultierende Zeitbegriff nicht eindeutig. Es muss nun untersucht werden, ob die Quantentheorien verschiedener Foliationen ('Eichungen') unitär äquivalent sind. Träfe dies zu, wäre die gewählte Foliation irrelevant. Erst spezielle Lösungen der Wheeler-DeWitt-Gleichung (wenn man den lokalen Beobachter wieder einführen muss) leiten wieder auf einen Ordnungsparameter, den man mit der Zeit identifizieren kann. Dies führte in der Vergangenheit zu der Frage nach einer 'Physik ohne Zeit'.
Lesehinweis
- Web-Essay: Was ist Zeit?
Siehe im Zusammenhang unter Planckscher Strahler.
 © Andreas Müller, August 2007
© Andreas Müller, August 2007
Index
ADAF
ADD-Szenario
ADM-Formalismus
AdS/CFT-Korrespondenz
AGB-Stern
Äquivalenzprinzip
Akkretion
Aktiver Galaktischer Kern
Alfvén-Geschwindigkeit
Alfvén-Zahl
Allgemeine Relativitätstheorie
Alpha-Zerfall
AMR
anthropisches Prinzip
Antigravitation
Antimaterie
Apastron
Apertursynthese
Aphel
Apogäum
Astronomie
Astronomische Einheit
asymptotisch flach
Auflösungsvermögen
Axion
AXP
Bardeen-Beobachter
Baryogenese
Baryonen
baryonische Materie
Bekenstein-Hawking- Entropie
Beobachter
Beta-Zerfall
Bezugssystem
Bianchi-Identitäten
Big Bang
Big Bounce
Big Crunch
Big Rip
Big Whimper
Birkhoff-Theorem
Blandford-Payne- Szenario
Blandford-Znajek- Mechanismus
Blauverschiebung
Blazar
BL Lac Objekt
Bogenminute
Bogensekunde
Bosonen
Bosonenstern
Boyer-Lindquist- Koordinaten
Bran
Brans-Dicke- Theorie
Brauner Zwerg
Brill-Wellen
Bulk
Casimir-Effekt
Cauchy-Fläche
Cepheiden
Cerenkov-Strahlung
Chandrasekhar-Grenze
Chaplygin-Gas
Chiralität
Christoffel-Symbol
CMB
CNO-Zyklus
Comptonisierung
Cosmon
C-Prozess
Derricks Theorem
de-Sitter- Kosmos
DGP-Szenario
Diffeomorphismus
differenzielle Rotation
Distanzmodul
Dodekaeder-Universum
Doppler-Effekt
Drei-Kelvin-Strahlung
Dunkle Energie
Dunkle Materie
Eddington-Leuchtkraft
Effektivtemperatur
Eichtheorie
Einstein-Ring
Einstein-Rosen- Brücke
Einstein-Tensor
Eisenlinie
Eklipse
Ekliptik
Ekpyrotisches Modell
Elektromagnetismus
Elektronenvolt
elektroschwache Theorie
Elementarladung
Energie
Energiebedingungen
Energie-Impuls-Tensor
Entfernungsmodul
eos
eos-Parameter
Epizykel
Ereignishorizont
erg
Ergosphäre
eV
Extinktion
Extradimension
extragalaktisch
extrasolar
extraterrestrisch
Exzentrizität
Fanaroff-Riley- Klassifikation
Faraday-Rotation
Farbindex
Farbladung
Farbsupraleitung
Feldgleichungen
Fermi-Beschleunigung
Fermionen
Fermionenstern
Fernparallelismus
Feynman-Diagramm
FFO
FIDO
Flachheitsproblem
FLRW-Kosmologie
Fluchtgeschwindigkeit
Frame-Dragging
f(R)-Gravitation
Friedmann-Weltmodell
Galaxie
Gamma Ray Burst
Gamma-Zerfall
Geodäte
Geometrisierte Einheiten
Geometrodynamik
Gezeitenkräfte
Gezeitenradius
Gluonen
Grad
Granulation
Gravastern
Gravitation
Gravitationskollaps
Gravitationskühlung
Gravitationslinse
Gravitationsradius
Gravitations- rotverschiebung
Gravitationswellen
Gravitomagnetismus
Graviton
GRBR
Große Vereinheitlichte Theorien
Gruppe
GUT
GZK-cutoff
Hadronen-Ära
Hamilton-Jacobi- Formalismus
Harvard-Klassifikation
Hauptreihe
Hawking-Strahlung
Hawking-Temperatur
Helizität
Helligkeit
Herbig-Haro- Objekt
Hertzsprung-Russell- Diagramm
Hierarchieproblem
Higgs-Teilchen
Hilbert-Raum
Hintergrundmetrik
Hintergrundstrahlung
HLX
HMXB
Holostern
Homogenitätsproblem
Horizont
Horizontproblem
Horn-Universum
Hubble-Gesetz
Hubble-Klassifikation
Hubble-Konstante
Hydrodynamik
hydrostatisches Gleichgewicht
Hyperladung
Hypernova
Hyperonen
Inertialsystem
Inflation
Inflaton
intergalaktisch
intermediate-mass black hole
interplanetar
interstellar
Isometrien
Isospin
Isotop
ITER
Jansky
Jeans-Masse
Jet
Kaup-Grenzmasse
Kaonen
Kataklysmische Veränderliche
Keine-Haare- Theorem
Kepler-Gesetze
Kerr-de-Sitter- Lösung
Kerr-Lösung
Kerr-Newman- de-Sitter- Lösung
Kerr-Newman- Lösung
Kerr-Schild- Koordinaten
Killing-Felder
Killing-Tensor
K-Korrektur
Koinzidenzproblem
Kollapsar
Kompaktes Objekt
Kompaktheit
Kompaktifizierung
Kompaneets-Gleichung
konforme Transformation
Kongruenz
Koordinatensingularität
Kopenhagener Deutung
Korona
Korrespondenzprinzip
Kosmische Strahlung
Kosmische Strings
Kosmographie
Kosmologie
Kosmologische Konstante
Kosmologisches Prinzip
kovariante Ableitung
Kovarianzprinzip
Kreisbeschleuniger
Kretschmann-Skalar
Krümmungstensor
Kruskal-Lösung
Kugelsternhaufen
Ladung
Lagrange-Punkte
Lambda-Universum
Lapse-Funktion
Laserleitstern
Lense-Thirring- Effekt
Leptonen
Leptonen-Ära
Leptoquarks
Leuchtkraft
Leuchtkraftdistanz
Levi-Civita- Zusammenhang
Licht
Lichtjahr
Lichtkurve
Lie-Ableitung
Linearbeschleuniger
LINER
Linienelement
LIRG
LMXB
LNRF
Lokale Gruppe
Loop-Quantengravitation
Lorentz-Faktor
Lorentzgruppe
Lorentzinvarianz
Lorentz-Kontraktion
Lorentz-Transformation
Lundquist-Zahl
Luxon
Machsches Prinzip
Machzahl
Magnetar
magnetische Rotationsinstabilität
Magnetohydrodynamik
Magnitude
marginal gebundene Bahn
marginal stabile Bahn
Markariangalaxie
Maxwell-Tensor
Membran-Paradigma
Mesonen
Metall
Metrik
Mikroblazar
Mikrolinse
Mikroquasar
Milchstraße
Minkowski-Metrik
Missing-Mass- Problem
mittelschwere Schwarze Löcher
MOND
Monopolproblem
Morphismus
M-Theorie
Myonen
Neutronenreaktionen
Neutronenstern
Newtonsche Gravitation
No-Hair-Theorem
Nova
Nukleon
Nukleosynthese
Nullgeodäte
Olbers-Paradoxon
O-Prozess
Oppenheimer-Volkoff- Grenze
optische Tiefe
Orthogonalität
Paralleluniversum
Parsec
partielle Ableitung
Pauli-Prinzip
Penrose-Diagramm
Penrose-Prozess
Pentaquark
Periastron
Perigäum
Perihel
periodisch
persistent
Petrov-Klassifikation
PG1159-Sterne
Phantom-Energie
Photon
Photonenorbit
Photosphäre
Pion
Pioneer-Anomalie
Planck-Ära
Planckscher Strahler
Planck-Skala
Planet
Planetarische Nebel
Poincarégruppe
Poincaré- Transformation
Polytrop
Population
Post-Newtonsche Approximation
Poynting-Fluss
pp-Kette
p-Prozess
Prandtl-Zahl
primordiale Schwarze Löcher
Prinzip minimaler gravitativer Kopplung
Protostern
Pseudo-Newtonsche Gravitation
Pulsar
Pulsierendes Universum
Pyknonukleare Reaktionen
Quant
Quantenchromodynamik
Quantenelektrodynamik
Quantenfeldtheorie
Quantengravitation
Quantenkosmologie
Quantenschaum
Quantensprung
Quantentheorie
Quantenvakuum
Quantenzahlen
Quark-Ära
Quark-Gluonen- Plasma
Quarks
Quarkstern
Quasar
quasi-periodisch
Quasi-periodische Oszillationen
Quelle
Quintessenz
Radiogalaxie
Radion
Randall-Sundrum- Modelle
Randverdunklung
Raumzeit
Rayleigh-Jeans- Strahlungsformel
Ray Tracing
Reichweite
Reionisation
Reissner-Nordstrøm- de-Sitter- Lösung
Reissner-Nordstrøm- Lösung
Rekombination
relativistisch
Relativitätsprinzip
Relativitätstheorie
Renormierung
Reverberation Mapping
Reynolds-Zahl
RGB-Bild
Ricci-Tensor
Riemann-Tensor
Ringsingularität
Robertson-Walker- Metrik
Robinson-Theorem
Roche-Volumen
Röntgendoppelstern
Roter Riese
Roter Zwerg
Rotverschiebung
Rotverschiebungsfaktor
r-Prozess
RRAT
RR Lyrae-Sterne
Ruhesystem
scheinbare Größe
Schleifen- Quantengravitation
Schwache Wechselwirkung
Schwarzer Körper
Schwarzer Zwerg
Schwarzes Loch
Schwarzschild-de-Sitter- Lösung
Schwarzschild-Lösung
Schwarzschild-Radius
Schwerkraft
Seltsamer Stern
Seltsamkeit
Seyfert-Galaxie
Singularität
skalares Boson
SNR
Soft Gamma-Ray Repeater
Sonne
Spektraltyp
Spezialität
Spezielle Relativitätstheorie
Spin
Spin-Netzwerk
Spinschaum
Spin-Statistik-Theorem
Spintessenz
s-Prozess
Standardkerzen
Standardmodell
Standardscheibe
Starke Wechselwirkung
Statisches Universum
Staubtorus
Stefan-Boltzmann- Gesetz
stellare Schwarze Löcher
Stern
Sternentstehung
Strange Star
Stringtheorien
Subraum
Supergravitation
supermassereiche Schwarze Löcher
Supernova
Supernovaremnant
Superstringtheorie
Supersymmetrie
Symbiotische Sterne
Symmetrie
Symmetriebrechung
Symmetriegruppe
Synchrotron
Synchrotronstrahlung
Synchrozyklotron
Tagbogen
Tardyon
Teilchen
Teilchenbeschleuniger
Tensorboson
Tensoren
Tetraden
Tetraquark
TeVeS
Thermodynamik
thermonukleare Fusion
Tiefenfeldbeobachtung
Tierkreis
TNO
Topologie
topologische Defekte
Torsionstensor
Trägheit
transient
Transit
Triple-Alpha-Prozess
T Tauri Stern
Tunneleffekt
ULX
Unifikation
Unitarität
Universum
Unruh-Effekt
Urknall
Vakuumstern
Vektorboson
Velapulsar
Veränderliche
Vereinheitlichung
Viele-Welten- Theorie
VLA
VLBI
VLT
VLTI
Voids
VSOP
Weakonen
Weinberg-Winkel
Weiße Löcher
Weißer Zwerg
Wellenfunktion
Weylsches Postulat
Weyl-Tensor
Wheeler-DeWitt- Gleichung
Wiensche Strahlungsformel
Wilson-Loop
WIMP
Wolf-Rayet-Stern
w-Parameter
Wurmlöcher
X-Kraft
X-ray burster
Yerkes- Leuchtkraftklassen
YSO
Yukawa-Potential
Zeit
Zeitdilatation
Zodiakallicht
Zustandsgleichung
Zustandsgröße
Zwerge
Zwergplanet
Zwillingsparadoxon
Zyklisches Universum
Zyklotron


 W
W
